Abstract
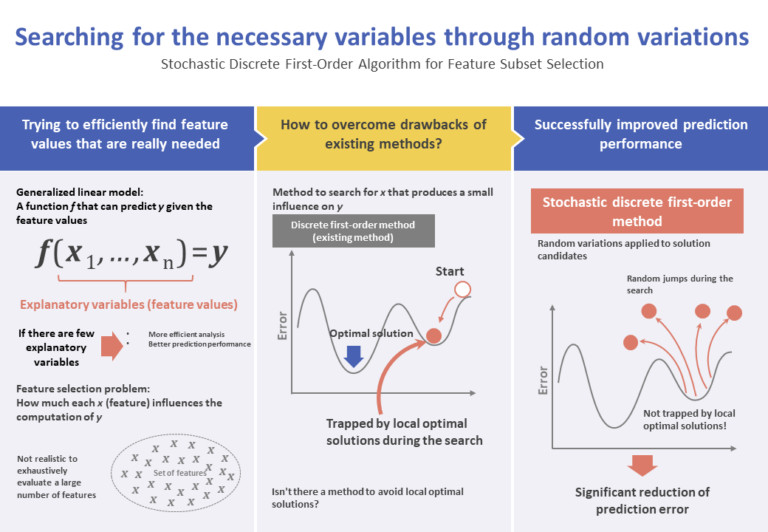
Background and issues
A generalized linear model is a model where the probability distribution of the residue belongs to the family of exponential distributions, including linear regression, logistic regression, Poisson regression, and others. Feature selection (as a problem) consists of selecting effective feature values (explanatory variables) during the creation of the predictive model. In recent years, feature selection using the mixed integer optimization technique has received increased attention.
Feature selection can reduce the cost of data collection and storage, making it possible to predict regression coefficients more efficiently. In addition, it helps to explain the causal relationship between selected features and the responses inferred by the regression model. It is possible to improve the predicting performance by eliminating redundant features.
A comprehensive method of finding the best subset of features is to evaluate the quality of every possible subset of features. However, this method is not feasible due to its computational load, except in the case of a small number of features.
Many previous research works focus on heuristic optimization algorithms, to address the problem of selecting large subsets. The most widely-known algorithm of this type is the step-wise method, which consists of repeating the addition or subtraction of a single feature at a time.
Various regularization methods for sparse prediction have been investigated recently, among which the most generally used is the Lasso method. In the Lasso method, the L1 regularization term is applied, which makes unused coefficients equal to zero.
Bertsimas et al. proposed a discrete first-order (DFO) method to efficiently find an approximate optimal solution for the feature subset selection problem. However, the DFO algorithm cannot escape traps resulting from local optimal solutions. In view of that, Bertsimas et al. propose that a random initialization be performed, with repeated executions of the DFO algorithm.
In the present research, we propose a stochastic discrete first-order method, which is an improved version of the DFO method. In this method, random variations are introduced in the candidate solutions in order to avoid local optimal solutions. In addition, in order to accelerate conversion, the optimal step size along the gradient descending direction is calculated. Moreover, in order to improve the predictive performance of the obtained model, a regularization term L2 is introduced.
Proposed method
The feature selection problem is formulated as follows. Consider n to be the number of samples, p the number of features, 𝒚 ∈ ℝn×1 the vector of response values (predicted values), 𝑿 ∈ ℝn×p a matrix containing the values of features (explanatory variables), and 𝜷 ∈ ℝp×1 the vector of partial regression coefficients. The multiple regression model can then be expressed as y = X𝜷 + e, where e is the prediction error.
The feature selection problem is an optimization problem, where a fixed number of features must be found that minimize e. In other words, the feature selection problem is:
minimize f(𝜷) := 1/2||y – X𝜷||22 (1)
subject to ||𝜷||0 ≤ k. (2)
Here, ||𝜷||0 is the number of non-zero elements of 𝜷 (i.e., the number of features) and k is the size of the desired subset, satisfying the condition < min {n, p}.
Discrete first-order method
The discrete first-order method, which is the usual method, can be described as follows
- Define threshold δ as a sufficiently small positive integer. Consider 𝜷(1) ∈ ℝn×1 satisfying ||𝜷(1)||0 ≤ k, with m ← 1.
- Update β. 𝜷(m+1) ∈ ℋk(𝜷(m) – 1/L∇f(𝜷(m))).
- If |f(β(m)) – f(β(m+1))| ≤ δ, then the algorithm is stopped, and β(m+1) is obtained as the solution.
- Return to step 1 with m ← m + 1.
Here, L is the Lipschitz constant related to the gradient of f. In other words, for all η, β ∈ ℝn×1, ||∇f(η) – ∇f(β)||2 ≤ L||η – β||2 is satisfied. From Equation (2), we have ∇f(β) = XTXβ – XTy.
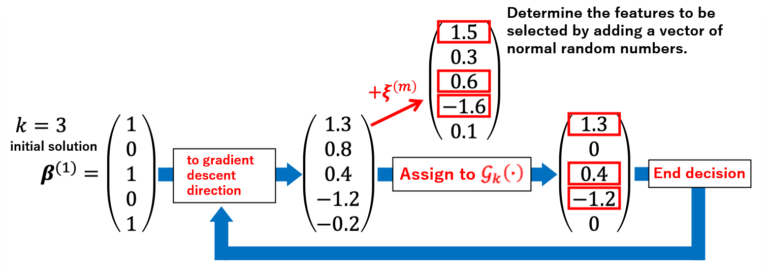
Moreover, ℋk represents an operator that converts all elements 𝑘 + 1 onwards to zero, when they are placed in descending order of absolute values (Figure 1). For instance, when β = (1.3, 0.8, 0.4, -1.2, -0.2)T and k = 3, the above, rearranged in descending order of the absolute values of β, is (1.3, -1.2, 0.8, 0.4, -0.2). ℋk(β) makes the elements k + 1 onwards of the rearranged set above equal to zero, resulting in ℋk(β) = (1.3, 0.8, 0, -1.2, 0).

Stochastic discrete first-order method
The proposed stochastic discrete first-order method improves step 1 of the conventional method, as follows.
- Update β. β(m+1) ∈ Gk(β(m) – 1/L∇f(β(m)) | ξ(m))
Here, ξ(m) ∈ ℝp×1 is a vector formed by independent, normal random numbers with an average of zero and a covariance 𝜎2m. Like ℋk, Gk is an operator that makes all elements 𝑘 + 1 onwards equal to zero when they are arranged in descending order of absolute values. However, it differs in the fact that a normal random number is added during the rearrangement (Figure 2). This procedure makes it possible to escape from local optimal solutions.
The proposed method also optimizes the displacement width along the search direction in order to accelerate convergence speed. In addition, a penalty term 𝐿2 is introduced in the target function in order to improve predictive performance.
Evaluation and demonstration
The effectiveness of the proposed method was demonstrated through an experiment using logistic regression. The experiment data are as follows.
Partial regression coefficients β0 = (1, 𝟎T, 1, 𝟎T,…, 1, 𝟎T)T ∈ ℝp×1.
Feature matrix 𝑿 ∈ ℝn×p. (It is generated using equal independent distributions Np (𝟎, 𝚺). The component (i, j) of the covariance matrix 𝚺 is 7|i-j|.)
Response vector 𝒚 ∈ ℝn×1
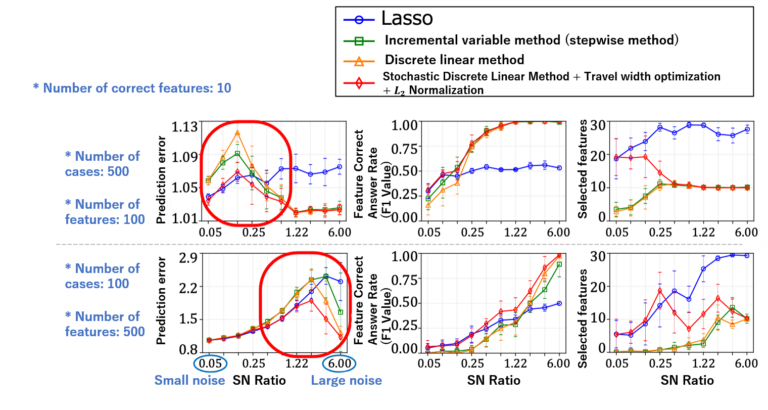
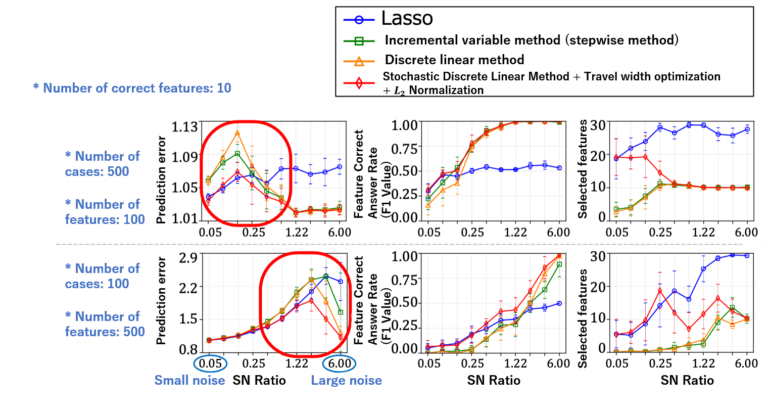
We obtained the correct answer ratios of prediction and features (F1 value: for the case where the correct features were selected), and the number of selected features, as evaluation parameters. We compared the predictive performance against other methods (Figure 3).
Results and proposal
In the present research, we proposed a stochastic, discrete first-order method to select a subset of the feature variables of a multiple regression model. In the proposed method, a random variation is applied to candidate solutions in order to avoid local optimal solutions. The optimal step size along the descending gradient direction was derived to achieve fast convergence, and a regularization term L2 was introduced to improve prediction performance.
According to simulation results, we verified that our method is able to significantly reduce out-of-sample prediction errors compared to the case where a randomly initialized, discrete first-order method is repeatedly executed. Moreover, our method yielded better accuracy than the Lasso and forward-stepwise methods, both in terms of subset selection and prediction.
In addition to the results above, it is worth noting that our method is extremely simple, and easy to understand and to implement. These features will make it appealing to researchers and data analysts in companies.


