筑波山における渋滞の原因とは？そう単純ではない渋滞問題に挑む！

　概要

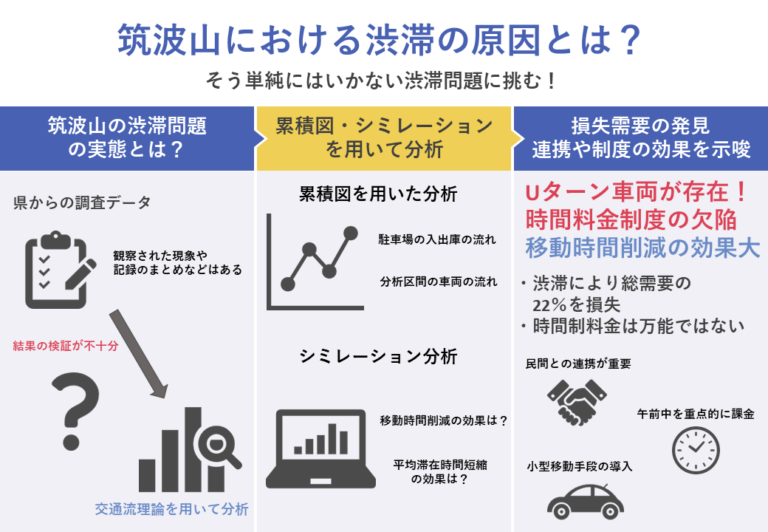
　背景と目的

全国各地の有名観光地では渋滞問題が多く発生しており，それによって経済損失や環境への負担の増加などの問題が起きている．
このような観光地の渋滞問題は本研究が対象とする筑波山でも繁忙期を中心に発生している．筑波山は多くの来訪者が移動手段として自家用車を利用して来訪すること，また地形の性質などから道路や駐車場構造に問題があること，がその大きな要因である．
県や市はこの渋滞を解消しようと取り組んでおり，これまでに様々な対策を実施してきたが解決に至っていない．
また，令和 2年に筑波山周辺渋滞対策協議会が開かれ，その一環として茨城県では令和 4 年度に筑波山の交通状態に関する調査を実施している．
この調査結果から駐車場の入庫待ち行列が渋滞原因であると定性的に述べることはできる．ただし，その原因となっている駐車場の容量（供給）と観光需要，そして渋滞との関係性が定量分析されているとは言い難い状態であった．
また，自分自身も筑波山にツーリングすることが多々あり，実際によくこの渋滞に遭遇していることからこの問題が身近に感じられ，興味を持っていた．
そこでこのテーマについて卒業論文として取り組むに至った．具体的には，本研究は筑波山の交通渋滞の実態を観測データと交通流理論に基づきより定量的に分析し，その対策を提案・評価することを目的とする．
提案の中身としては道路拡張や新規駐車場開設といった多額の予算がかかり非現実的なハード面のものではなく，低予算で実施することができるソフト面での対策を検討する．具体的には現在一律である駐車場料金を時間変動時間変動制にする，交通規制などを行うといった対策を検討する．

　手順

本研究は以下の三段階で構成される．

第一段階：交通流理論に基づき観測データを分析することで，渋滞の実態を需要面・供給面の双方から明らかにする．
第二段階：渋滞の主原因と特定された駐車場について詳細に分析し，その利用状況モデルを構築する．
第三段階：構築したモデルを用いたシミュレーション分析を通して，主に駐車場における料金設定などの施策を検討する．

　使用データ

調査概要

利用するデータは行楽シーズン中の令和4年5月4日に行われた交通実態調査で取得されたものである．調査当日の天候は晴れ，調査時間は7:00～15:00の8時間である．
調査内容は交通量調査，渋滞長調査，ナンバープレート調査の三種類あり，その内容はそれぞれ，交差点における通過車両台数や車の進行方向の記録，交差点を起点とする渋滞長や滞留長の計測，駐車場の入庫・出庫台数と来訪車のナンバープレート記録，などである．
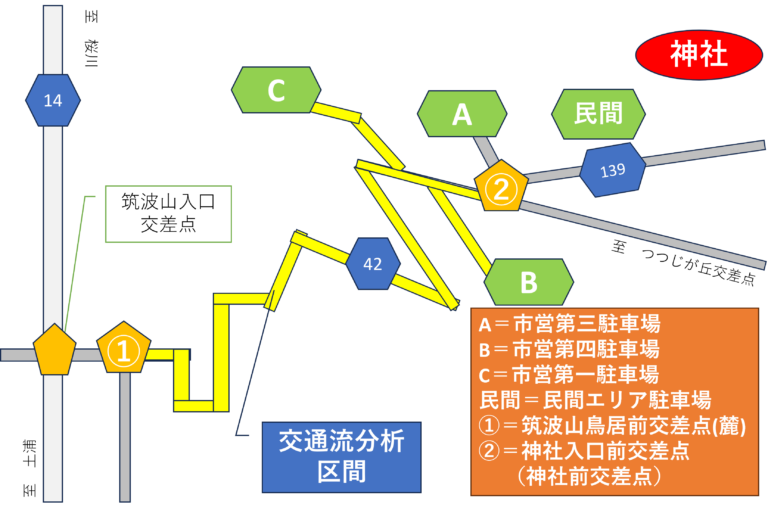
これらの調査位置全体図と本研究で分析対象とする筑波山鳥居交差点及び神社入口前交差点の位置は図１に示すとおりである．
筑波山神社周辺の自動車専用駐車場は，三か所の市営駐車場と複数の民間の駐車場（以下民間エリア駐車場と一括りにする）から構成される．
駐車場の位置関係は，神社に近い順に民間，第三，第四，第一駐車場となっている．これ以降，市営駐車場の名称を神社に近い順にA，B，C駐車場とする（図１参照）．また図１の筑波山鳥居前交差点を麓，神社前入口交差点を神社前交差点とそれぞれ呼ぶ．

調査結果

茨城県が行った交通実態調査の結果のうち，本研究に関わるものについて述べる．

図２は県道42号線のうち，麓から神社前交差点までの区間（図１の黄色い道路を指す，以下この区間を分析区間とする）の入山方向の旅行時間の推移を表したものである．
この図をみると9時以降に旅行時間が増加し，ピークを11時前後に迎えていることが分かる．この時の旅行時間は約80分前後であった．そしてその後旅行時間は減少傾向にあることから渋滞が解消に向かっていったことが読み取れる．
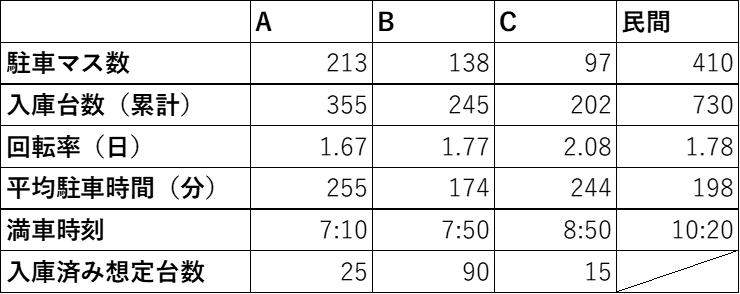
また下の表１は，駐車場の利用に関する調査結果をまとめたものである（駐車場容量は大型車を除く)．

　渋滞分析

累積曲線を用いた渋滞分析

図３，4は分析区間の累積図である．累積図とはある地点を通過した車両の累積台数を時刻ごとに表示したものである．これらの図では麓が流入点，神社前交差点とB，C駐車場の入庫方向が流出点となる．

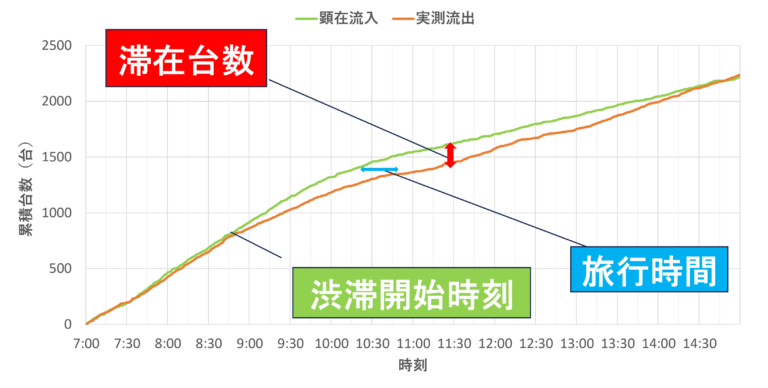
累積図は同時刻の流出曲線と流入曲線の台数の差が分析区間の存在台数を表しており，同じ累積台数の時刻の差が地点間の旅行時間を表す．また2つの曲線が乖離し始める時刻が渋滞開始時刻となる．なお上記の存在台数は分析区間が一本道とみなせるためほぼ渋滞台数と一致する．
この累積図は交通現象，特に駐車場や高速道路のインターなどを通過する車両の流れ，すなわち需要などを捉えるのに役立つ基本的な手法である．

ここで図3より，7時半ごろから2曲線が乖離し始めることからこの時間帯から旅行時間が伸び始めることが分かり，その後その乖離幅は11時ごろにピークを迎え，ピーク後はその幅が狭まっていくことから旅行時間が短くなっていくことが読み取れる．これは図２の調査結果と概ね合致する．
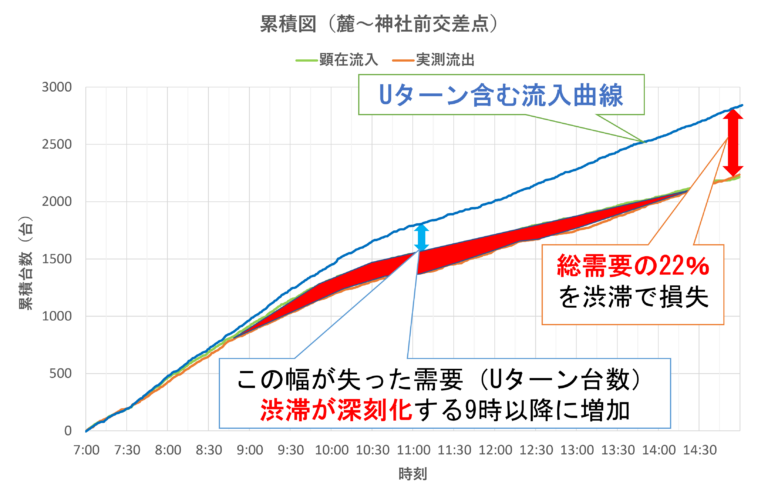
ここから図４を見ていく．図4の3つの曲線のうち，顕在流入曲線（青線）と流出曲線（水色線）は，通常の流入・流出曲線を表しており，潜在流入曲線（赤線）は流入はしたものの神社前交差点にたどり着く前にUターンし，再び麓を通過した車両台数を顕在流入曲線に足したものである．
また図4の曲線のうち，麓を通過し神社前交差点まで実際に行った累積台数を顕在需要，麓は通過したもののUターンした車両台数も含めた累積台数を潜在需要とすると，これらの差は約630台と分かる．これは潜在需要の約22％を占める．
ここで，潜在流入曲線と顕在流入曲線の乖離は8時以降に始まり，渋滞が深刻化する9時以降にさらに広がることから潜在需要と顕在需要の乖離は，麓を通過したものの渋滞で神社方面に行くことを諦めた車両が発生したことが原因と推察される．
次にこの累積図から分析できる渋滞損失時間について述べる．渋滞損失時間とは渋滞によって車両が被った遅れ時間のことである．
この時間に時間価値を掛けることで渋滞によって失われた損失額を算出することができる．観光交通の時間価値として一人/分あたり28.87円[2]，乗員は一台当たり二人として損失額を試算した．
その結果，渋滞損失時間は18.45分/台，損失額は約239万円となった．一方潜在需要を想定すると渋滞損失時間は約58分/台，損失額は約954万円であった．

駐車場と累積図の関係

最後に各駐車場の満車時刻と渋滞との関係性について分析・考察する．

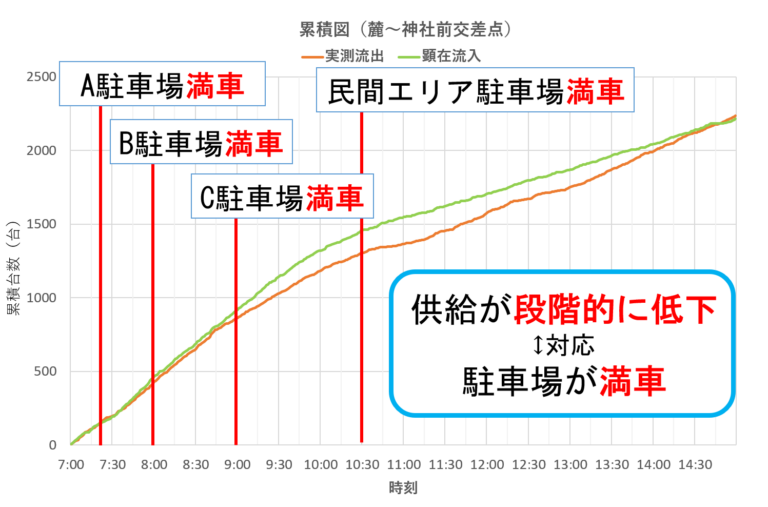
図5や表１を見るとまず7時１０分ごろにA駐車場が満車になり，次に8時前ごろにB駐車場が満車になるが，この時刻の図5をみると2つの曲線が乖離していることから渋滞が始まったことが分かる．
また9時前ごろにC駐車場が満車になるとその乖離幅が開く，つまり渋滞が深刻化しているということも分かる．
他にも10時半前ごろに民間エリア駐車場が満車になるときに流出曲線の傾きが緩やかになっているが，これは民間駐車場の入庫待ち行列が神社前交差点まで延伸してしまい，交差点の先が詰まってしまうことが原因である．
以上のことより，図3などの流出曲線の傾きが緩やかになっていること，つまり供給が段階的に低下している現象が駐車場の満車現象と対応している，つまり駐車場が渋滞の原因であるということが定量的に言える．

　駐車場の利用状況

ここからは先程渋滞の原因と判明した駐車場について分析する．

定常状態と出庫率

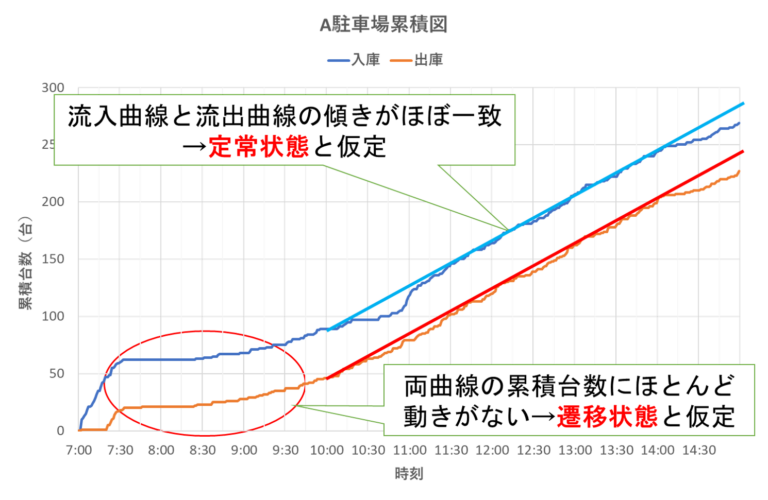
図6はA駐車場における累積図である．この流入・流出曲線の推移を見ると，最初は二つの曲線の増え方に差がみられるがある時刻を境に両方ともほぼ同じ台数増加するようになっていることが分かる．
これは駐車場が満車になり，かつ出庫する車がある程度存在する，つまり駐車場の入出庫の流れが一定の流率で回っている状態を表す．例えば図6では10時以降がこの状態に当たる．本研究ではこの状態を定常状態と呼ぶ．
一方で同図の7時30分から定常状態前の時間帯を見ると入庫・出庫曲線の累積台数が伸びていないことが分かる．この状態を（定常状態への）遷移状態と呼ぶ．
上記の定常状態では待ち行列理論のリトルの公式を用いることができる．

ここでリトルの公式とは，以下の公式で表せる．
L=λW
ただし，Lはシステム内にいる車両数，λは車両の到着率，Wは平均滞在時間を表す．

そして本分析ではLを駐車場容量，λを駐車場の出庫率，Wを平均利用時間とすると，以下の関係式が成り立つ．
平均利用時間＝駐車場容量÷出庫率
これは以降の渋滞対策を検討する際のモデル式となる

分析結果

以上の式から駐車場の平均利用時間を推定した結果が表２である．

この表から，駐車場の平均利用時間は神社（観光地入口）までの距離が長いほど長くなっていることが分かる．
ここで，筑波山の現況では入庫待ち車両は空いた駐車場にすぐに入るというFirst-In-First-Outの状態になっているため，各駐車場に入庫した車両の滞在時間の分布は駐車場によって変わらないと考えられる．
すなわち，各駐車場における観光地滞在時間は等しく，平均利用時間の差は駐車場から筑波山神社までの移動時間の差であると解釈できる．
よって，神社に一番近いA駐車場を基準とすれば，観光地滞在時間の平均値は200分，B，C駐車場から神社までの移動時間はそれぞれ20分，100分と推定される．

　渋滞対策の分析

分析の設定

ここでは定常状態になった後の平均滞在時間，各駐車場から神社までの移動時間を変更したとき，どの程度渋滞が改善されるかを分析する．
前者は料金制度（具体的には時間料金制）によって調整可能，後者は新モビリティ導入施策によって削減可能であると考えられる．
本分析では次の4つの条件のもと分析を行った．
- A：全ての駐車場の移動時間を0分に仮定
- B：平均滞在時間のみ変更
- C：AとB条件の組み合わせ
- D：Cの条件に民間駐車場も考慮

分析結果

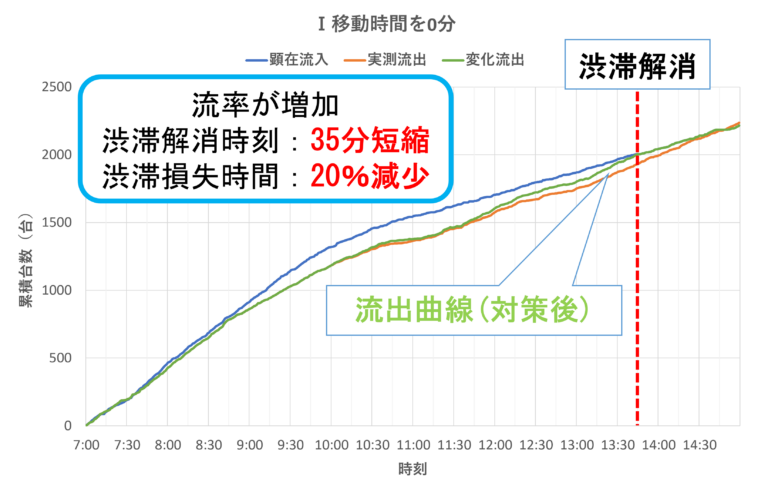
まず条件Aの下，分析を行った結果が図7である．この図を見ると流出率が増加し13時45分ごろに渋滞が解消されたことが分かる（現況では渋滞解消時刻は14:20分）．
このときの渋滞損失時間は14.76分/台であり，現況の18.45分/台から3.69分/台減少，割合にして20％も減少している．このことは移動時間の削減には大きな渋滞削減効果があることを示している．

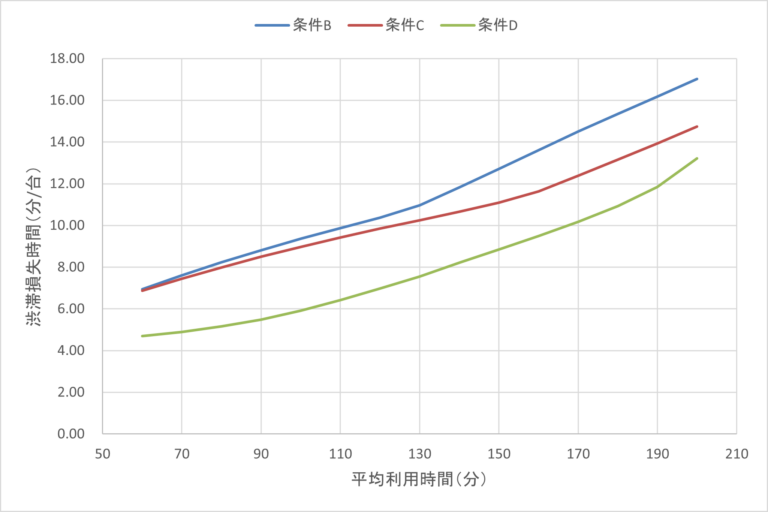
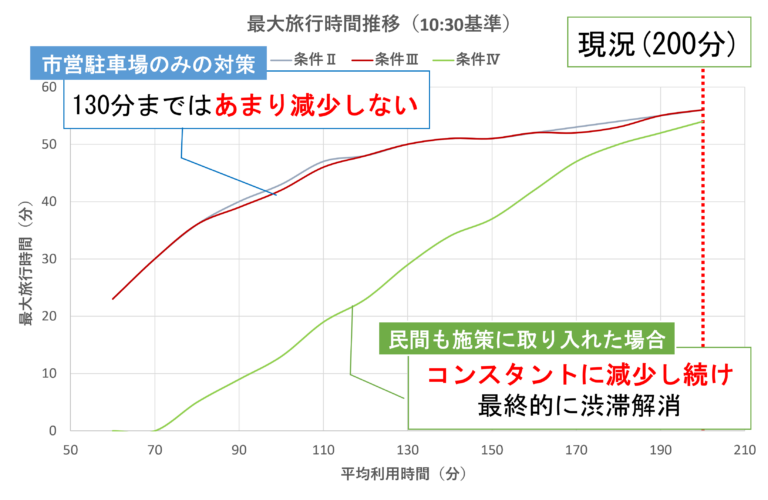
図8，図9は，条件B～Dの下行ったシミュレーション分析の結果として得られた，渋滞損失時間及び最大旅行時間の推移を示したものである．この最大旅行時間は渋滞のピークである10時30分時点の分析区間の旅行時間のことを指す．
図8より，まず条件B，Cの下では，平均利用時間が減少すると渋滞損失時間もほぼ線形に減少していくことが分かる．しかし，その減少幅は次第に小さくなっていく．
これは，平均滞在時間を変更したとしても定常状態に至るまでの遷移状態での出庫率は依然として低いままであり，その主な効果が渋滞ピーク以降に限定されてしまうためである．このことは図9の条件B，Cの最大旅行時間が減少しづらいことからもわかる．
一方で，駐車場容量の最も多い民間駐車場も含めた条件Dでは，渋滞損失時間の減少も大きく，かつ最大旅行時間もほぼ線形に減少している．
以上のことから，時間料金制度を市営駐車場だけに導入してもその効果は限定的であり，民間駐車場との連携が重要であることが分かる．
具体的には渋滞損失時間を現況から半減するには市営のみ対象の料金制度だと平均滞在時間を110分も減らす必要があるのに対し，民間も対象にすると50分減らすだけで済むという大きな効果の違いがある．

　終わりに

研究成果

本研究では筑波山における渋滞対策を提案・評価することを目的として，観測データに基づく渋滞の実態把握，渋滞要因である駐車場のシミュレーションモデルの構築，それに基づく渋滞対策分析を行った．

その結果，以下のことが明らかとなった．

渋滞によって失ってしまった需要，すなわち筑波山へ入山することを諦めた車両数は630台，総需要のうち約22％にも達する．
渋滞による損失時間・損失価値はそれぞれ18.45分/台，約239万円にもなる．
駐車場の定常状態ではリトルの公式を用いてモデル化することができる．
駐車場から観光地入口までの距離に応じて平均利用時間が長くなる．
駐車場と観光地間の移動時間を0分にすることで渋滞損失時間は20％削減可能である．
時間料金制度を市営駐車場だけに導入してもその効果は限定的であり，民間駐車場との連携が重要である．

渋滞対策の提案

本研究結果を踏まえて渋滞対策を検討する．

まず平均滞在時間に関する対策としては

定常状態への移行を早めるために午前中を重点的に課金する
長時間利用者の公共交通の利用を促進する
民間駐車場も対象とする時間制料金制度

といった対策が考えられる．次に移動時間に関する対策では、そもそも移動時間を削減するだけでも渋滞改善効果があることを踏まえて

移動時間を短縮するために小型移動手段等の導入
道路拡幅などが難しい場合、交通規制を行いモビリティ用の道路を確保

といった対策が本研究結果から考えられる．

　後記

何事も疑うことが大事

後記として筆者がまず書きたいことは，研究するうえで大事なことは疑うことだということである。分析結果は当然，理論的に導き出される予測結果と違う結果となった場合，何が原因かということを疑いながら探索していくことになるが，研究を行っていくと時には分析結果だけでなく，その基となるデータも疑う必要が出てくる．

実際本研究でも図３の累積図を算出する際，調査個所別のデータセットで分析すると理論的に異常な状態になってしまい，どうしたものかと悩んだ．結果として全ての調査個所のデータが入ったデータセットで分析すると理論通りの結果が算出され，両者のデータを見比べてみると個別データの方で車両の走行方向が逆に登録されているデータが数多く見つかった．

このように，データも人間が収集している場合，間違える可能性があるので，最初から完全に信用せずに様々なことに対して疑いの目をもつことが重要であることを学んだ．

研究することの楽しさ

本研究の結果として個人的に印象に残っていることは，累積図から渋滞によりUターンをして帰ってしまう車両，つまり渋滞により損失してしまった需要があることを発見したことである．このことは県の調査結果には記載されていない．

この調査結果は一見してなんとなく十分だと感じられるが，理論に基づき分析してみるとそれまで誰も気づけていなかった新事実がこのように判明することがあるということを実際に体験することができた．

また，研究前では現在一律料金である駐車場料金を単純に時間制料金に変更すればこの渋滞問題は簡単に解決すると思っていたが，結果が示す通りそう単純ではないといったことが分かり，改めて渋滞問題の解決の難しさを感じた．

このように新事実を発見するという研究の醍醐味をまだまだ研究者としては未熟な筆者でも体験することができた．読者の皆さんも卒論等で研究を行うときにはただ研究するのではなく，この醍醐味を味わいながらと取り組んでほしいと思う．

　参考文献

[1] 茨城県　令和4年度GW　筑波山周辺交通実態調査　2022.
[2] 道路事業の評価手法に関する検討委員会:時間価値原単位等の計算方法について:第4回道路事業の評価手法に関する検討委員会　資料2　pp4　2008.