取り組みの概要
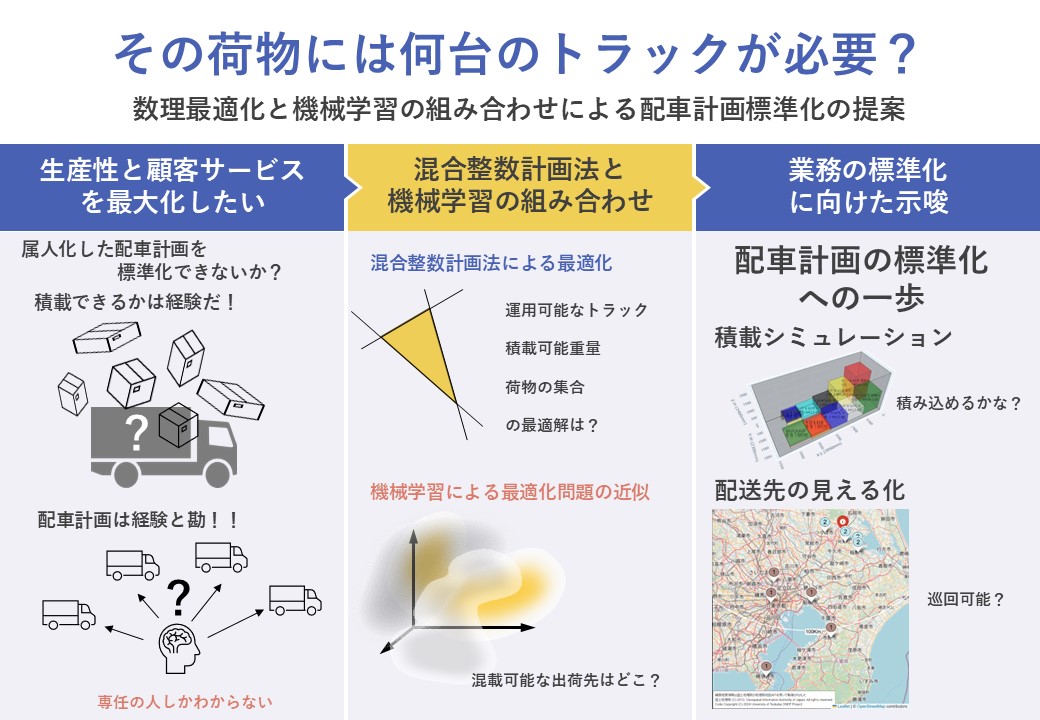
背景と課題
物流を取り巻く現状
経済産業省の、産業構造審議会 商務流通情報分科会 流通小委員会 第1回報告 “物流を取り巻く現状と取組状況について”[1]によれば、
貨物1件あたりの貨物量が直近の30年で約3分の1まで減少する一方、物流件数はほぼ倍増しており、物流の小口・多頻度化が急速に進行している。
とある(図1)。つまり、昨今の EC サイトやフリマアプリによる個人間取引の拡大を主な要因として、増加した取扱個数とともに、小口化してでも迅速に配送しようとする、顧客サービス向上を進めた結果と考えられる。また、ドライバーの労働時間が規制される、いわゆる2024年問題の対策として、積載効率を上げて対応しようとする動きも2020年頃より見られるが、依然として、貨物自動車の積載率は40%以下の厳しい水準である。
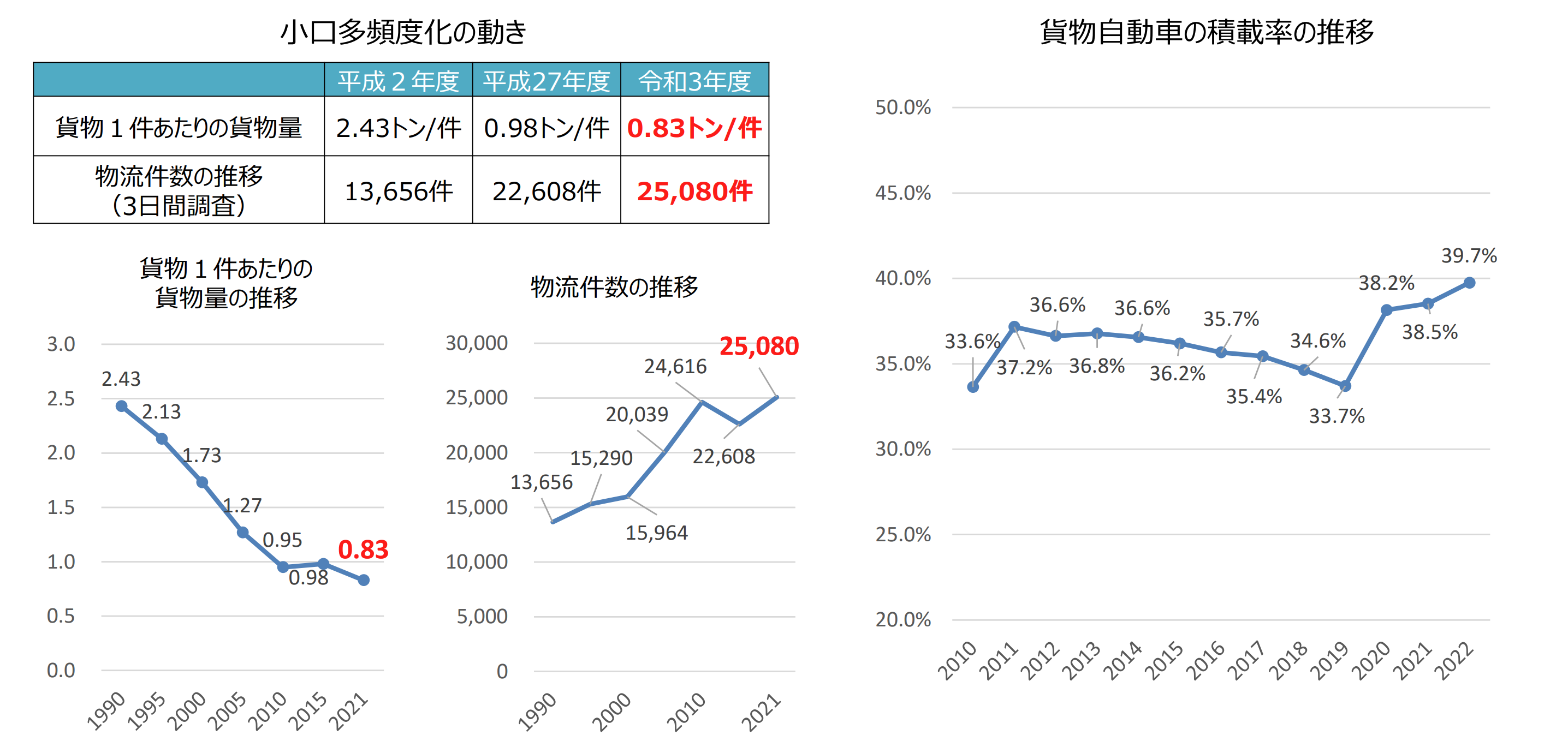
図1 トラック積載率について、出典[1]:経済産業省、産業構造審議会 商務流通情報分科会 流通小委員会 第1回報告より
一方、パートナー企業の現状は、出荷量の季節的な変動が顕著に見られ、特に夏場に低く年末年始に向けて増加する傾向がある。また、月曜と金曜に出荷が集中し、4トン~10トンを用いた出荷回数が最も多く、次いで10トン~20トンであり、4トン以下は少ない。なるべく大型トラックに混載して積載効率を上げようとする傾向と、コストの小さい中型を使用して現場ごとに迅速に出荷する傾向の、両方が存在する。前述したように、2024年問題なども考慮すれば、トラック業界の人材確保も難しくなると考えられるため、積載効率を上げ、使用するトラック台数の削減を目的とすることは、社会的にも意義があると考える。
目的と目標
企業の要求として、現場側からは、現在手作業で行っているトラック配車を手早く自動化したいという意見と、トラック使用台数を削減したいという意見が多かった。加えて、トップ層からは、生産性と顧客サービスの最大化を目的として、属人化した業務を自動化したいという意向が見られた。これらの階層の異なる要求を、最終手段に落とし込むために、要求事項の整理と現状把握を行い、実現可能なソリューションとして、相関を示したものが、次の出荷フローボトルネックと手段の提案である。
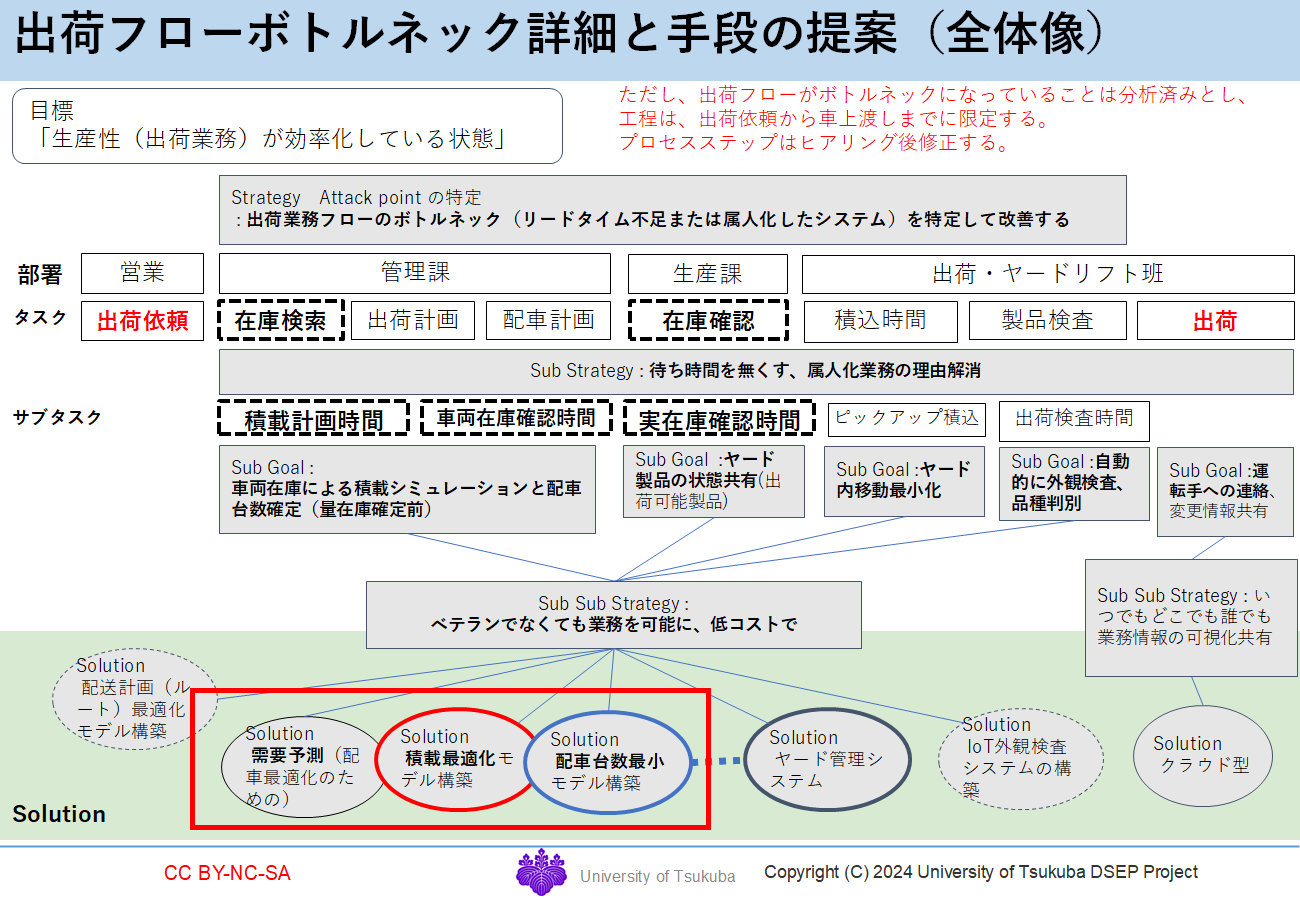
図 2 出荷フローボトルネックと手段の提案
これによれば、最終的な戦略は、「ベテランでなくても業務を可能に、低コストで」実施できる施策になる。この戦略を基に、ヒアリングから提案したソリューションの中で、相互に関連する、需要予測、積載最大化、配車台数最小化を選択し、最上位目的を、トップ層の要求を満足する、“属人化している配車計画を標準化すること”とし、その目標を、“代替可能なレベルのシステム構築”とした。本報告では、これらに内在する課題を解決する手段として、特に数理最適化と機械学習を用いた手法について検討し、配車台数を最小化しようとする積載計画を行った結果を考察する。
実験方法
手法の選定と概説
一般的な最適積み付け計画システムまたは配送計画の文献について調査した[2]。その中で、最適解が求められ、Python用のライブラリが普及していてコード化が容易な、整数線形計画を、第一に考慮してコード化を進めた。しかしながら、積載の制約条件を加えると計算が収束しなくなったため、制約条件を3段階に分けて、問題点が明確になるように実験を進めた。以下、各段階について説明する。
1段目として、まず最も普遍的である積載重量を制約条件とし、目的関数をトラック台数の最小化にした最適化を、整数線形計画法で行う[3]。使用可能なトラックの集合は、時刻ごとに変化する可能性があるため、緒仕様を入れたトラックの定義リストをマスターとして用意し、積載したトラックの状態を、逐次マスターに反映させつつ計算する。一巡で最適解が見つからない状態を回避するために、トラックマスターは4巡目まで用意し、実際に何回運用するかの判断は人が行う。また、優先順位の高い順(または運用コストの低い順)に指定可能とした。
2段目は、1段目で重量が最適化された荷物の集合を、指定されたトラックの積載寸法を制約条件として、First Fit法で積載できるかどうか計算させる。枕木および釣りボルトは、使用不使用およびサイズに関係なく一律で追加した。その他、First Fitの基本ルールとして、重量が重い順に、トラック前方から見て右手前位置を基準点として、幅方向、長さ方向、高さ方向の順に優先配置とした。また、製品特性上、横倒しなどの回転は禁止、低面積が同じか小さいものは、上に積重ねられるものとした。各品種における積重ねの組み合わせが個別制約条件として入るが、詳細な記述は省略する。
3段目として、出荷先を複数まとめた、いわゆる混載を検討した。2段目の積重ねが、要求された制約条件とルールの基で、正しく機能して初めて、荷物の混載が可能かどうかが判断できる。混載のためのまとまりは、簡易的に、機械学習のk-meansクラスタリング手法を用いて、相互間の距離が近しいものをクラスターとするように、出荷拠点からの直線距離と角度の関数として計算した。
実験手順
既に実績のある過去の出荷データを用いて、トラックを再配分するシミュレーションを実行し、結果を実際の使用台数と照合していただいた。出荷管理情報をベースに、製品の寸法を製品規格から取得し、車両情報と合わせて最適処理を行い、配車積載リストとして出力した。今回は、シミュレーションのため、過去の出荷情報を使用したが、実際には、出荷依頼のあった時点のリストを基にして計算することを前提にしている。
実験結果
積載重量の最適化では、各トラックは、問題なく最大重量内に近く荷物が配分された。ただし、台数最小化を目的関数としたため、積載重量の大きいトラックを使用する傾向が見られた。この最適化計算は、重量のみの制約条件であるため組み合わせが少なく、数秒以下で完了した。
積算可能の確認では、トラックの荷台を模倣した空間に、製品規格の寸法から直方体で仮定した荷物を、First Fit法で配置した。図 3に、荷物配置・積重ね実施例を示す。X軸が長さ方向で、X軸原点が運転席側を示す。運転席側から順に重量物(大きいもの)が並べられ、同寸以下の製品は積重ねられていることが確認できる。
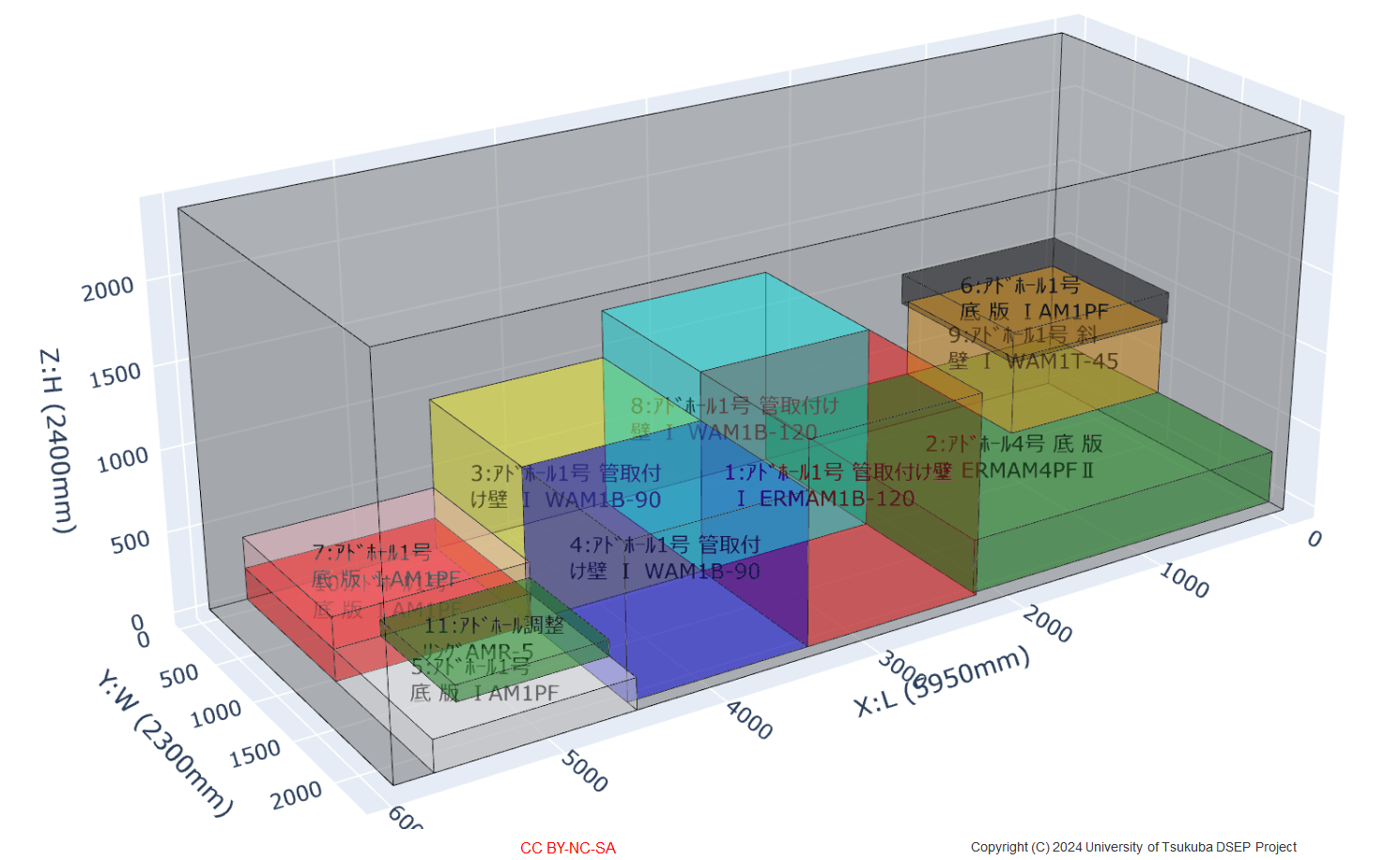
図 3 荷物配置・積重ね実施例
混載の確認には、クラスター化した出荷先の情報を地図上に示した。図 4に、生成したクラスターの例を示す。緯度経度の取得は国土地理院の地図APIまたはNominatimを用い、地図の表示はOpenStreetMapを用いた。丸の中の数字がクラスター番号を示している。クラスター数は仮に3とした。市名までの住所によってクラスタリングしているため、1か所に複数の出荷先が含まれる。赤で示したラベルは拠点となる事業所である。
図 5に、k-meansによるクラスターの生成例を示す。横軸に距離を縦軸に出荷拠点からの角度を示す。クラスター0は、拠点からの距離はほぼ同等に近い位置にあるが、方角が若干異なることが判る。拠点から近い場合、方角が異なっても巡回できる可能性が高く妥当である。一方で、クラスター1は、方角は似ているが、拠点からの距離が異なっている。この場合、拠点から近い順に巡回できる可能性もあるので、一見妥当と思われるが、しかし、地図上で見ると、遠距離になるにしたがって出荷先の距離が離れており、東京湾を挟んで逆方向なので、これらの巡回は現実的には難しいと思われる。
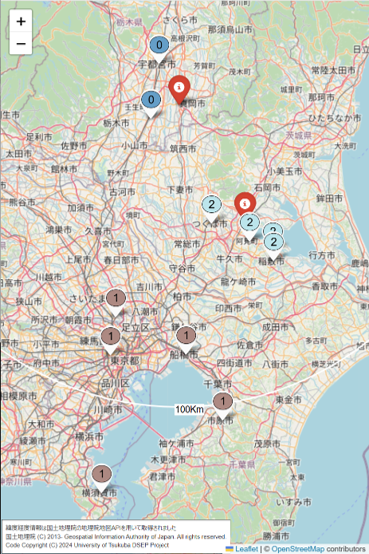
図 4 生成したクラスターの地図上表示例
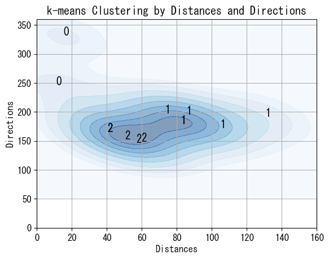
図 5 k-meansによるクラスター生成例
(https://www.openstreetmap.org/copyright/en 地図データはOpenStreetMapの貢献者から提供されており、使用条件はリンクのライセンスに従います)
考察
数理最適化は整数線形計画法を用い、オープンソースのPuLP[4]またはOR-Tools[5]を採用したが、重量制約の次に、寸法と積載の制約条件を入れると、計算が収束しない問題が発生した。制約の次元数が増えることで、計算量が飛躍的に増大したものと推定されるが、特に、荷物の配置位置をミリ単位で入力したことが解の検索に影響したものと思われる。代替え案として、多段階に分けて計算する方法を採用した。
1段目の重量で最適解であっても、2段目の積み方で積載できない場合が多いことが判明した。つまり、重量よりも体積の影響が大きい製品群であると推定されるが、これは、ヒューム管が中空であることを考えると合理的に説明できる。また、3段目の混載可能かどうかも、積重ね条件に左右される。従って、2段目の積載における段積みの可能性を正確にコード化し、積載効率を最大にできるかどうかが、台数削減のカギを握る。しかしながら、この部分は慣例的なルールが多く存在し、コード化に時間を要することが判明した。段積みの条件を無視して可能な限り空きスペースに積む方法で計算し、最終的な判断は現場で行う方法の提案も受けたが、積みきれない場合のリスクもあるので保留とした。
3段目の出荷先のクラスタリングでは、時間の都合上、簡易的に距離と方角を基準としてk-meansで分割を行ったが、直線距離であるため、東京湾を挟んで、神奈川と千葉の市川市が一つのクラスターにされるなどの弊害も見られた。また、類似の方角と判断されても、遠距離になると離れるため、距離を対数スケールに変換することで走行時間の代替とする可能性もある。実用上は、走行予定ルートや到着時刻を考慮したクラスタリングの導入が必要になる。このクラスタリング手法の評価指標は、積載効率の向上に大きく寄与すると考えられ、今後の研究テーマとして取り組む価値があると考える。
おわりに
数理最適化と機械学習を組み合わせて、多段階の解法とすることで、属人化している企業の配車計画を、実用可能な計算時間で標準化する検討を行った。その結果、実際に配車した台数が11台であったところを、12台で積めるところまでは計算させることができた。既存の台数まで効率化することは一歩及ばなかったものの、各解法の段階における課題を明らかにし、計算に不足する変数を特定できたことで、業務の標準化に向けた一歩を達成したと考える。
製品の重ね方や複数出荷先の混載など、想定したよりも、慣例的かつルールベースの作業手順が多く存在したため、一律にコード化することは難しかった。そこで、先に全体のフレームワークを構築して、シミュレーションを回しながら徐々に最適化を進めることで、内在していた課題を浮き彫りにし、最終的に「到着時刻枠付き局所ルート巡回問題」であると特定した。この問題は、局所の決定方法において、時系列で変化する環境(例: 経路の交通状況や時間帯による需要変動)を変数としてクラスタリングに組み込むことが、ルート最適化や到着時刻管理の精度向上に必須である。さらに、少数の教師データを基に自己教師あり学習を活用することで、経時的な変動や外的条件を考慮した柔軟なルート設計の実現が可能であると考えられる。
後記
企業や自治体の実務専門家との議論を通じて、現場で求められるのは「実装可能で実用的な解法」であることを学び、実装しやすいシステム設計も課題として浮上した。また、現実的なプロジェクトの実行には、考え込んで正解を求めるという姿勢よりも、まず自ら試してみて広く議論する、という柔軟な姿勢が必要であると考えるので、もう少し積極的に行動した方が得るものが最大になったのではないかと思う。総じて、仮決めで採用したアルゴリズムをコード化した部分が多いため、複数のアルゴリズムを比較できるだけの余裕があれば良かったと思う。
参考文献
[1] 経済産業省, 物流を取り巻く現状と取組状況について, https://www.meti.go.jp/shingikai/sankoshin/shomu_ryutsu/distribution/pdf/001_01_00.pdf , 最終参照日2024年12月15日
[2] Zhao, X., Bennell, J.A., Bektaş, T. & Dowsland, K. 2016, “A comparative review of 3D container loading algorithms”, International transactions in operational research, 23, no. 1-2, pp. 287-320.
[3] 矢野夏子,航空貨物コンテナの最適詰め込みと大都市災害における緊急物資の最適配送計画,”第19回RAMPシンポジウム論文集, 2007″,139-149
[4] PuLP, https://pypi.org/project/PuLP/ , 最終参照日2024年12月15日
[5] Google OR-TOOLS, https://developers.google.com/optimization/install/python/pkg_windows?hl=ja , 最終参照日2024年12月15日
[6] Py3dbp, https://github.com/enzoruiz/3dbinpacking , 最終参照日2024年12月15日


