研究の概要

背景と課題

• タクシードライバーの月間労働時間は全産業平均と比較して約11%長いが、年間賃金水準は同比で約36%低いなど、その待遇の見直しが課題といえ、営業効率の改善も求められている

• タクシーのGPSデータから、実車率向上に寄与する行動パターンを検出することは有用と思われる
• タクシー経路の分析について、関連研究としては、タクシー需要のヒートマップをニューラルネットワークにより定量化したもの（Yao et al., 2018）、区画ごと通過回数を要素とした疎行列によりタクシー経路を表現して主成分得点を用いて経路を分析したもの（Ma et al., 2019）、スパース自己符号化器などの特徴埋め込み手法を用いてタクシー経路をベクトル化したもの（Huang et al., 2019）等がある
• 一方で、売上が高いドライバーは、時間帯ごとに行動を変えていることが報告されており、時間帯を考慮したタクシー経路の定量的分析が必要と考えられる

​↓

本研究では、タクシーの経路を表すグラフの各頂点（タクシーの位置情報を意味する、ただし8分の1地域メッシュ: 1辺が約125mに割り当て）に時間帯の情報を付与した、時間付加グラフのベクトル表現を提案した
この時間付加ベクトル情報を利用して、実車率を目的変数とした回帰分析を実行して、どのような経路ベクトルが実車率向上に寄与するかを検証、さらにタクシー経路のクラスター分析を実施し、有効なタクシーの経路パターンを見出した

※実車率 :=1勤務における実車時間/1勤務における総勤務時間
ただし、1勤務は各ドライバーについて、記録間隔が3時間未満で連続している区間とした

分析

分析データ

データ名称	タクシープローブ（GPS軌跡）データ
データ提供者	経営科学系研究部会連合協議会主催「令和元年度データ解析コンペティション」にて提供されたデータ
データ記録期間	2016年4月1日～2018年3月31日
データ収録内容	会社ID、ドライバーID、数十秒の間隔で日時、車両の状態（実車、空車、回送など）、緯度・経度等
分析経路総数	13,239通り

※原データには、タクシー会社7社の記録が含まれていたが、本研究では途中で記録が途絶えた会社や記録時間の間隔が長い会社を除いた3社（ドライバー89人）を分析対象とした
※データの前処理として、連続勤務時間が4時間以下または24時間以上の勤務は異常値としてデータから削除、また、記録時間の平均間隔が100秒以上の勤務は情報が不正確であるためデータから削除した

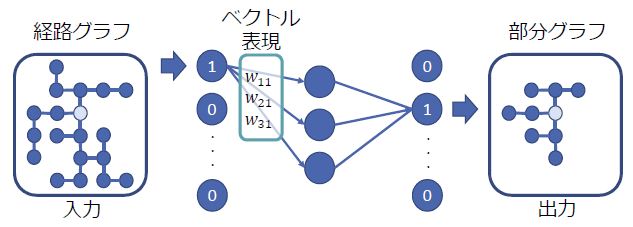
• ドライバーの日常的な行動パターンをとらえるため、連続する100乗車の空車時のタクシー経路をグラフ化、8分の1地域メッシュを頂点（ノード）とし、メッシュ間を移動した場合に辺（エッジ）が張られる
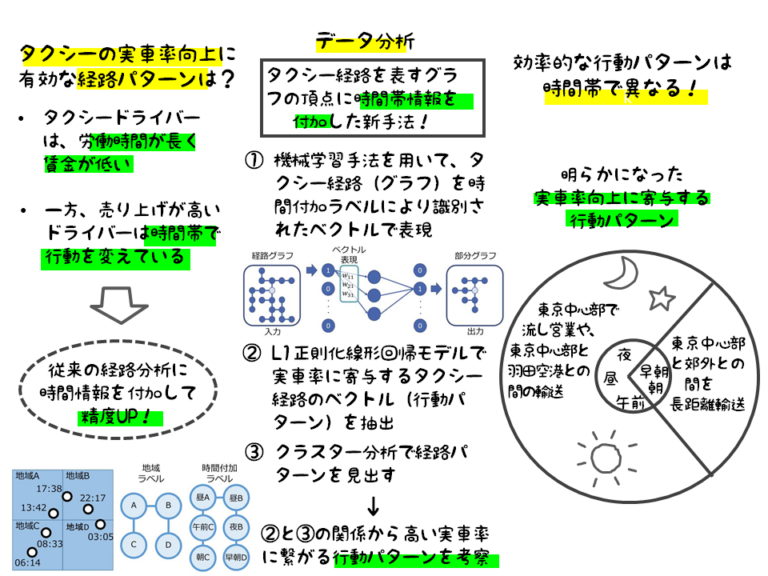
• グラフを数量化する方法としてPythonのライブラリgraph2vec（Narayanan et al.、 2017）を改変しつつ利用し、2層の（一つの中間層：ユニット数64をもつ）ニューラルネットワークによって、入力となる元の経路グラフと、出力となる部分グラフ（グラフ内の全てのノードを根とした任意の深さのグラフの集合）を与え、特徴ベクトルを求めた（図1）
• 各ノードを識別するためのラベルとして、単に次数（ノードに接続するエッジの数）を用いる「次数ラベル」、位置情報を反映する目的で地域メッシュIDを用いた「地域ラベル」、時間帯ごとに行動を変えることの有効性を検証するため、朝: 6～8時、午前: 8～13時、昼: 13～21時、夜: 21～翌3時、早朝: 3時から6時の5時間帯（各時間・各地域メッシュに何台空車タクシーがいるか？を変数にクラスター分析した結果に基づいて決定）と地域メッシュとを組み合わせた「時間付加ラベル」を用いた（図2）

分析1: 実車率の回帰分析

• どのような経路ベクトルが、高い実車率と関連するのかを調べるため、目的変数を各ドライバーの連続する4勤務日における平均実車率（ロジット変換したもの）、説明変数を「タクシー経路ベクトル」、および総勤務時間、各月の勤務回数、各曜日の勤務回数、各形態の勤務回数といった「勤務日の情報」としたL1正則化線形回帰モデル（Lasso）で分析を行った
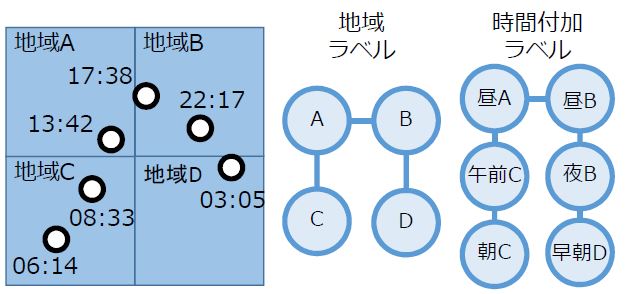
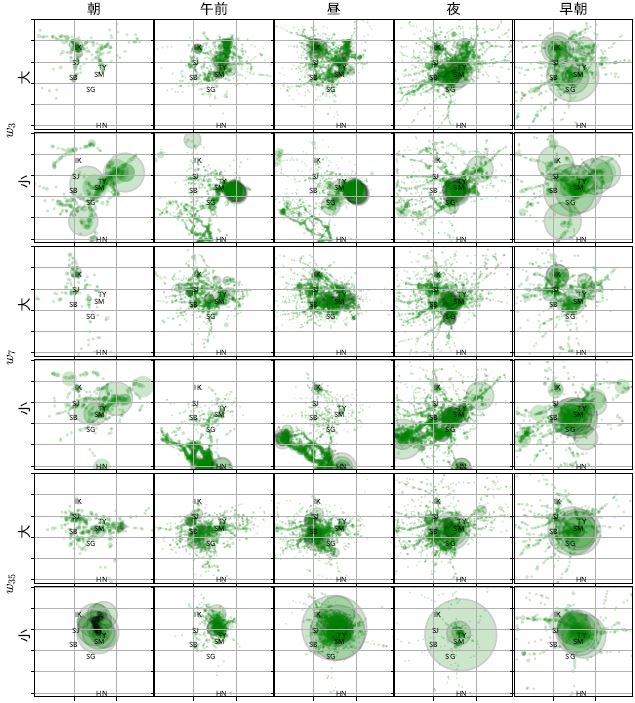
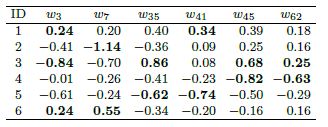
  →「タクシー経路ベクトル」については、時間付加ラベルを用いたモデルが最も予測精度が高かった
• 時間付加ラベルを用いたLassoにより選択された6個の説明変数（タクシー経路ベクトル）のみを用いて、さらに最小二乗法（正則化項を含まない）により偏回帰係数を推定したものが表1であり、説明変数の値が大きい / 小さいタクシーの経路を例として図示すると、図3のようになった（円の大きさは記録回数を表す）
  →たとえば、説明変数w3の値が大きい経路（図3の1行目）では、午前・昼に東京駅の北側を中心に流し営業（街中を走りながら乗客を探す行動）をしている経路といえ、逆に変数の値が小さい経路（図3の2行目）は時間帯によって拠点を変えながら付け待ち営業（駅や空港などのタクシー乗り場で乗客を待つ行動）をしているといえる
  ⇒このように、高い実車率に関連するタクシー経路の要素がわかった

分析2: タクシー経路のクラスター分析

• 最適なタクシー経路のパターンを探るため、時間付加ラベルを用いて生成した64次元のタクシー経路ベクトルを、Ward法（平方ユークリッド距離で算出）によるクラスター分析で分類した
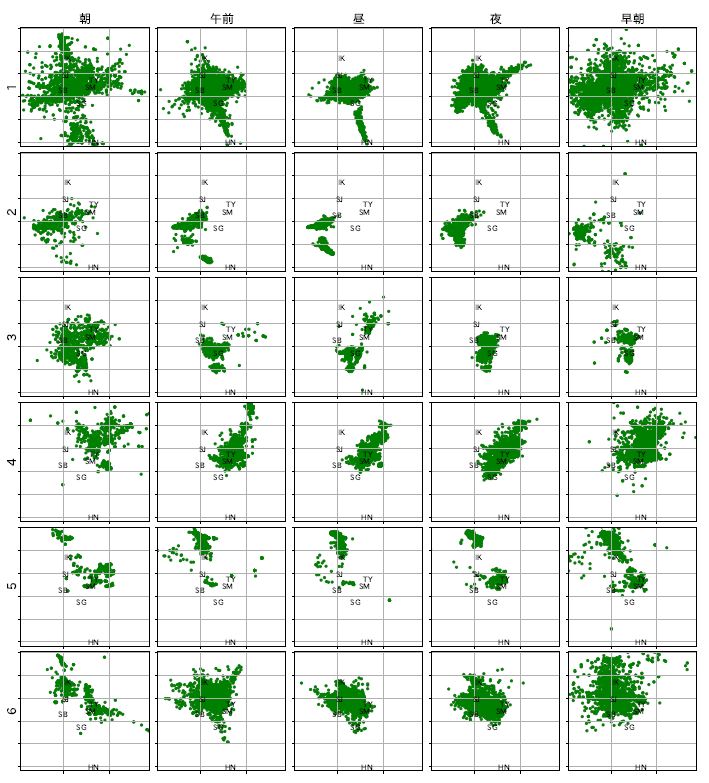
  →分類結果として、6種類のクラスター（経路パターン）が見出された（図4）

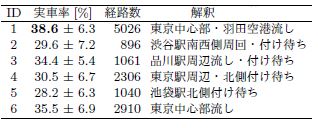
• ​分析1で選択された6つのベクトルと各クラスターの関係を見たものが表2、各クラスターの解釈は表3のようになった
  →たとえば、平均実車率の最も高かったクラスター1では、朝は経路の中心座標が広範囲に分布しているが、昼にかけて東京中心部へまとまり、早朝にかけて再び広がっていて、説明変数w3、w41の値が最も大きいことから、主に流し営業をしていると考えられる。
  また、午前から昼の時間帯には中心座標が羽田空港から東京中心部へ連なるように分布しており，この地域で長距離輸送をしていることが示唆される
  ⇒このように、高い実車率に関連する時間帯ごとのタクシー行動パターンがわかった

成果

• 偏回帰係数の分析結果と、比較的実車率の高いクラスター1とクラスター6の分析結果を踏まえると、以下のような行動が実車率向上に寄与すると考えられる。

早朝から朝	東京中心部と郊外との間を長距離輸送
午前から夜	東京中心部で流し営業や、東京中心部と羽田空港との間の輸送

レファレンス

Q. Ma, H. Yang, H. Zhang, K. Xie and Z. Wang, “Modeling and analysis of daily driving patterns of taxis in reshuffled ride-hailing service market,” Journal of Transportation Engineering Part A: Systems, 145, 2019.
H. Yao, F. Wu, J. Ke, X. Tang, Y. Jia, S. Lu, P. Gong, J. Ye and Z. Li, “Deep multi-view spatial-temporal
network for taxi demand prediction,” arXiv:1802.08714, 2018.
Z. Huang, G. Shan, J. Cheng and J. Sun, “Trec: An efficient recommendation system for hunting passengers with deep neural networks,” Neural Computing and Applications, 31, pp. 209–222, 2019.
A. Narayanan, M. Chandramohan, R. Venkatesan, L. Chen, Y. Liu and S. Jaiswal, “Graph2vec：Learning
distributed representations of graph,” arXiv:1707.05005, 2017.

この記事は、下記の論文を要約したものです

河上 佳太（2021）時間付加グラフのベクトル表現を用いたタクシー軌跡データの解析、2020年度 筑波大学 大学院 博士課程 システム情報工学研究科 修士論文