交通信号は何をターゲットにして制御すべきか？ – 筑波大学データサイエンス・ケースバンク

研究の概要

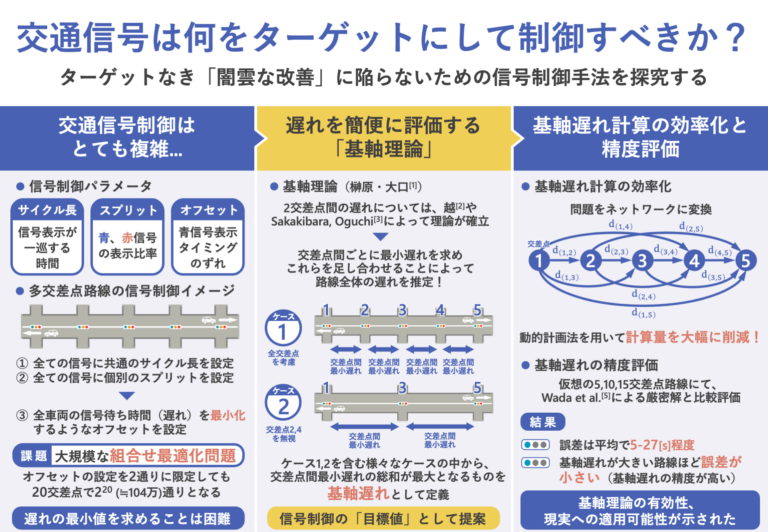
背景と目的

都市部の信号交差点では、交通の安全と円滑を図る観点から、信号群を相互に連動させる系統制御が行われている。
信号制御パラメータには、主なものとしてサイクル長（信号表示が一巡する時間）、スプリット（青、赤信号の表示時間比率）、オフセット（隣接信号間の青信号表示タイミングのずれ）の3つが挙げられる。
系統制御では、まず全ての信号に(1)共通のサイクル長を設定し、(2)個別にスプリットを設定した上で、(3)双方向に走行する全車両の遅れ（信号待ち時間）を最小化するようなオフセットを設定する手法が取られている。

一般に、信号交差点の数が大きくなればなるほど系統制御は複雑になる（組合せ最適化問題）。
図1のような多交差点路線においてオフセットを制御する状況を考えよう。このとき、オフセットの組み合わせは交差点数によって指数関数的に増大する。例えば、1交差点あたりのオフセットの設定をわずか2通りに限定したとしても、20交差点では2²⁰（約105万）通りを超えてしまうこととなる。
このような状態で、遅れの最小値（以下、最小遅れ）と、それを与えるオフセットパターンを厳密に求めることは困難である。

この問題に対して榊原・大口^[1]は、越^[2]やSakakibara, Oguchi^[3]によって定式化された2交差点間の遅れ式を用いて、多交差点路線における最小遅れの近似解を簡便な計算によって導出できることを示した。
- その上で、得られた近似解を「基軸理論最小合計遅れ」（以下、基軸遅れ）と定義し、これを系統制御が目指すべき目標値として用いることを提案した。
- 基軸遅れによって信号制御のパフォーマンスを簡便に評価することが可能となるため、特に実務において有用となる可能性がある。

その一方で、榊原・大口の基軸理論は素朴な方法論に基づいており、以下のような課題が残されている。
- 基軸遅れの計算に指数関数時間がかかる。具体的には、20交差点を越えると計算量の増大によって導出が困難となる。
- 基軸遅れの精度が評価されていない。厳密解と十分近似していれば意味を持つ指標であるが、そもそも厳密解を見つけることがかなり難しい。
そこで本研究は、榊原・大口が提唱した基軸理論の特性分析を通して、理論の有効性、現実への適用可能性を明らかにすることを目的とする。

既存理論

2交差点間を対象とした理論

越は、図2のような2交差点間において、需要の等しい双方向交通が存在する単純な状況を仮定し、車両1台当たり平均の最小遅れd_minと、リンク長L、サイクル長C、系統速度（制限速度）Vの関係を定式化した。

式から、リンク長（交差点間距離）Lによって、オフセットを適切に設定することで遅れを十分に減らせる場合と、オフセットを適切に設定しても遅れをほとんど減らせない場合があることが明らかとなった。
遅れに対するオフセットの感度を系統効果と呼び、前者の場合系統効果が「高い」、後者の場合系統効果が「低い」と表現される。

多交差点路線を対象とした理論：基軸理論

Newell^[4]は、3交差点以上で構成される路線では、路線全体の遅れに影響を与える交差点と、そうでない交差点が混在することを述べている。
Sakakibara, Oguchiは、路線全体の遅れは、系統効果の低い距離関係にある任意の2交差点間で生じる遅れの総和によってほぼ説明できると述べている。

この2つのロジックを組み合わせて、路線全体の最小遅れを簡便に推定してみよう。例えば、図3の5交差点路線の最小遅れを見積もりたいとする。

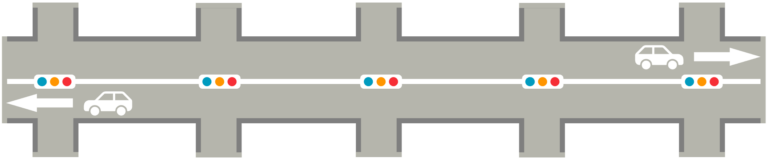
一見すると、図4（ケース1）のように全ての隣り合う交差点間に2交差点の理論式を独立に適用し、それぞれの最小遅れの総和を取れば、路線全体の最小遅れをうまく推定できそうである。
- しかし、隣り合う交差点間距離の系統効果が高い場合は、路線最小遅れをかなり過小に見積もることになる。
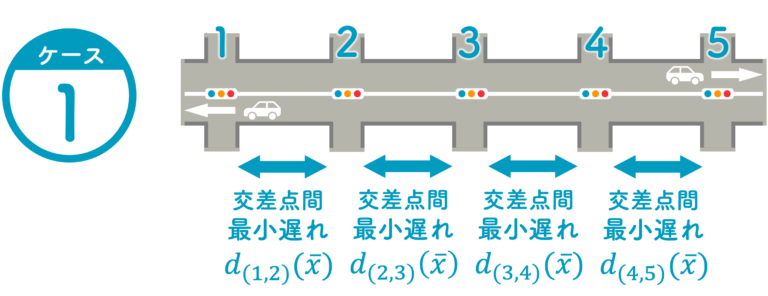
一方、交差点1-3, 3-5が系統効果が低い距離だとすると、その間の交差点を無視した図5（ケース2）のような状況を考え、この交差点間に2交差点の理論式を適用し、それを足し合わせたものは、最小遅れの近似として妥当であると言える。

このような形で、存在する全ての組み合わせに対して、
- 路線内の任意の2交差点間に生じる遅れを網羅的に計算し、
- その総和が最大となる組み合わせを取ることにより、
- 路線全体で「避けられない遅れ」を見積もる
図3の5交差点の場合、存在する全ての総和の組み合わせは図6のように示される。

総和d_sumの中で最大のものを「基軸遅れd_P(I_P)」、これらを与える交差点群を、路線全体の遅れに寄与する「基軸交差点I_P」と呼ぶ。
交差点数nの場合、総和d_sumは2^n-2通り存在する。
- したがって、全ての組み合わせに対して遅れを網羅的に計算し、その中から最大のものを選ぼう（全探索）とすると、交差点数nによって指数関数的に増加していくことに留意する必要がある（指数関数アルゴリズム）。

動的計画法を用いた計算の効率化

本章では、基軸遅れの計算に指数関数時間がかかるという課題に対して、問題をネットワークとして表現し、動的計画法を適用することで、これを多項式時間で解けることを示す。
まず、前節で説明した問題をネットワークとして表現することを試みる。そこで、図7のように、交差点1, 2, … , nをノード、各交差点同士の組み合わせをリンク、交差点間最小遅れd_(a,b)(x̅)をコストとみなす。

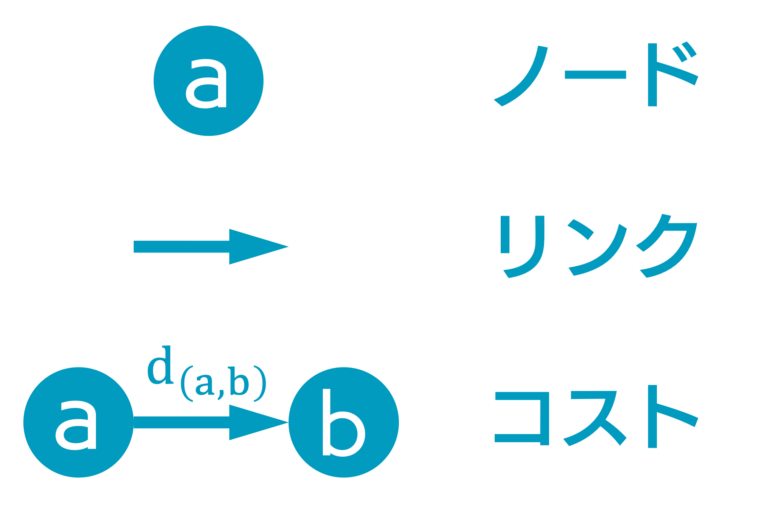
このとき、総和d_sumは、単一基点である交差点1から、単一終点である交差点nに向かうリンクのコストをそれぞれ足し合わせることによって求められる。例として5交差点の場合の、d_sumの数式表現とネットワーク表現の対応を、図8に示す。

図8のネットワークを1つにまとめると、図9のように表される。

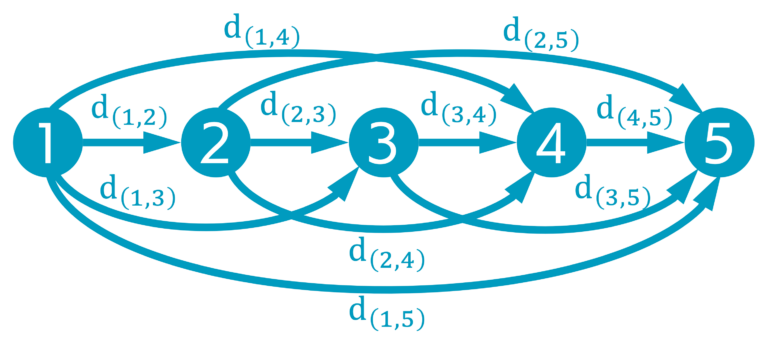
このネットワークを観察してみると、(i)向きを持つ、(ii)閉路がないという特徴があることがわかる。
- したがって、d_sumからd_P(I_P)を選ぶ問題は、有向非巡回グラフにおける最長経路問題とみなすことができ、図10のように各コストを-1倍することで、最短経路問題に置き換えることができる。

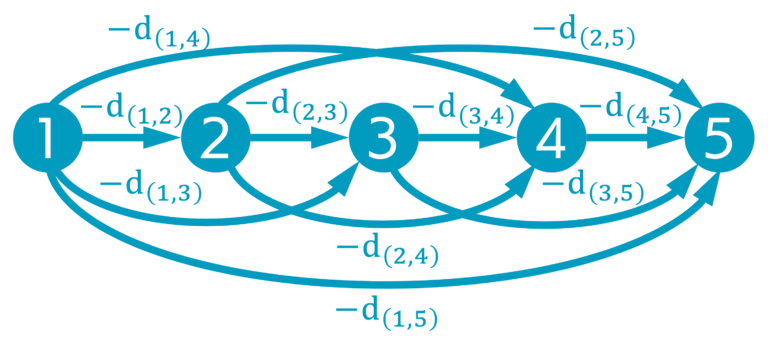
さらにこのネットワークを観察すると、全てのノードがあらかじめ(iii)終点ノードの方向に向いている(i.e., トポロジカルソートされている)という特徴があることが分かる。
- したがってこの最短経路問題は、動的計画法のアルゴリズムを用いて極めて効率的に解くことができる。計算量オーダーはO(n²)となる。
d_sumを全探索してd_P(I_P)を求める場合と、動的計画法を用いてd_P(I_P)を求める場合の計算回数を比較すると、5交差点以上のとき後者の方がより少ない計算回数となり、交差点数が大きくなるほど両者の差は増大していく。表1に両者の計算回数の比較を示す。

表1　計算回数の比較

交差点数	全探索（榊原・大口）	動的計画法（提案）
3	4	6
5	17	15
10	300	55
15	8296	120
20	262333	210
30	268435890	465

精度評価

Wada et al.^[5]は、交通流のダイナミクスを交通流の変分理論(VT : Variational Theory)で記述し、さらに信号制御パターンを「オン（青）・オフ（赤）」の2パターンとして表現することで、複雑な信号制御問題を0-1混合整数計画問題として明瞭かつ単純に定式化できることを示した。
Wada et al.の問題を解くことによって導かれる「オン・オフパターン」により、具体的な最適制御パラメータ（サイクル長・スプリット・オフセット）が生成される。このうち、サイクル長、スプリットに制約を加えることにより、基軸理論と同じオフセット最適化の枠組みで、遅れの比較分析を行うことができる。
本章では、都市部街路を模した300の仮想路線を対象に、基軸遅れとWada et al.に基づく最小遅れの厳密解をそれぞれ導出し、両者の差（近似誤差）について分析する。なお、厳密解の導出には膨大な計算を要するため、本研究では商用の数理最適化ソルバーであるGurobi Optimizerを利用している。

対象路線

対象路線は、ランダムな青時間とリンク長を持つ5交差点路線、10交差点路線、15交差点路線の計300路線である。
具体的には、共通サイクル長Cを120[s]、路線両端交差点の青時間g₁, g_nを48[s]、系統速度Vを50[km/h]、需要率Pを0.4に設定した上で、両端以外の交差点の青時間を48[s]から84[s]の範囲で、リンク長を80[m]から200[m]の範囲で、それぞれランダムに設定する。
- これらの設定は、榊原・大口の検討条件と同様のものであり、また15交差点については、榊原・大口で示されたケース1と同一の路線である。
対象路線の平均路線長は、5交差点が559.5[m], 10交差点が1260.7[m], 15交差点が1948.8[m]である。

計算結果

計算結果を図11（5交差点），図12（10交差点），図13（15交差点）に示す。
図11, 図12, 図13から、全300路線のうち298路線において基軸遅れが厳密解を下回ることが分かる。このことから、榊原・大口による検証とほとんど一致する結果が得られた。

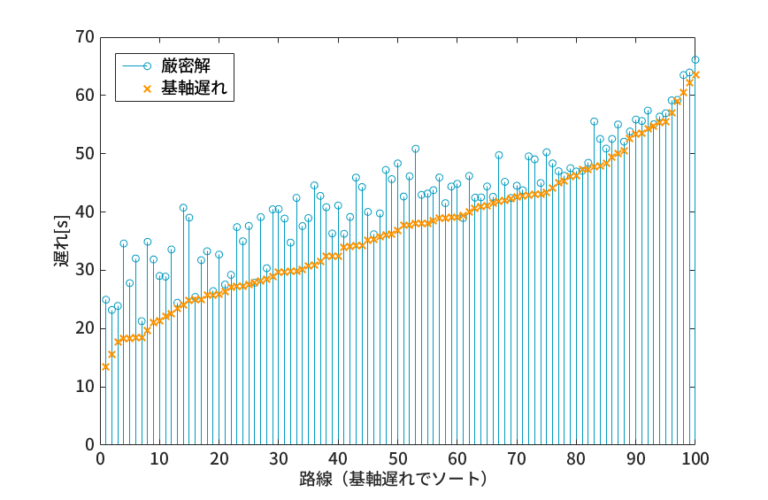
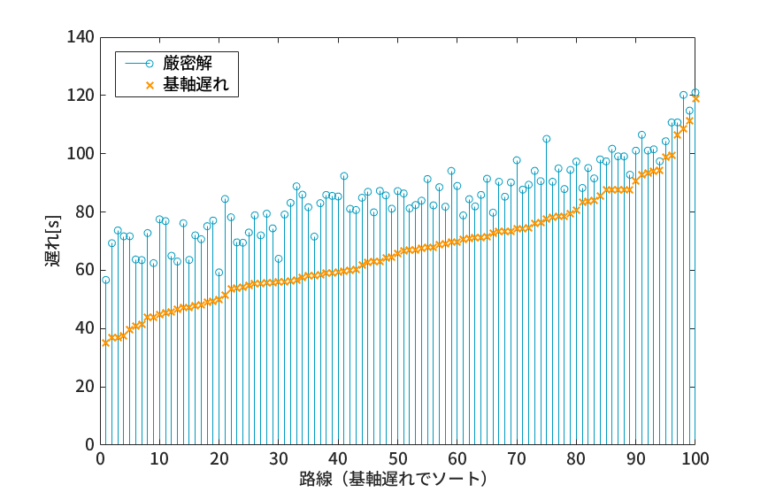
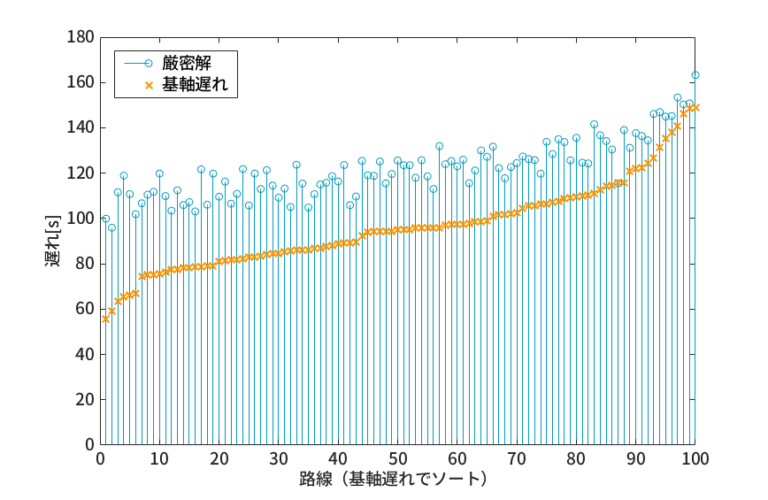
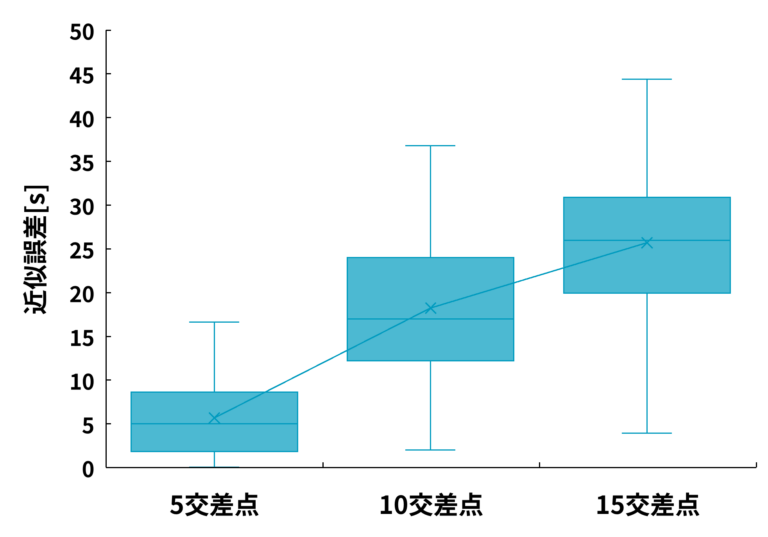
近似誤差の分布を図14に示す。近似誤差の平均は5.67[s]（5交差点），18.24[s]（10交差点），25.71[s]（15交差点）に、中央値は4.99[s]（5交差点），17.00[s]（10交差点），25.95[s]（15交差点）となった。
図14から、交差点規模が大きくなるにつれて、近似誤差が全体的にかつ平均的に大きくなることが分かる。ただし、（今回の路線条件において）共通サイクル長が120[s]であることを考慮すると、近似誤差はサイクル長に対して平均で5-21[%], 最悪でも40[%]程度に収まることから、基軸遅れは大規模路線においても一定の精度を保証しているものと考えられる。

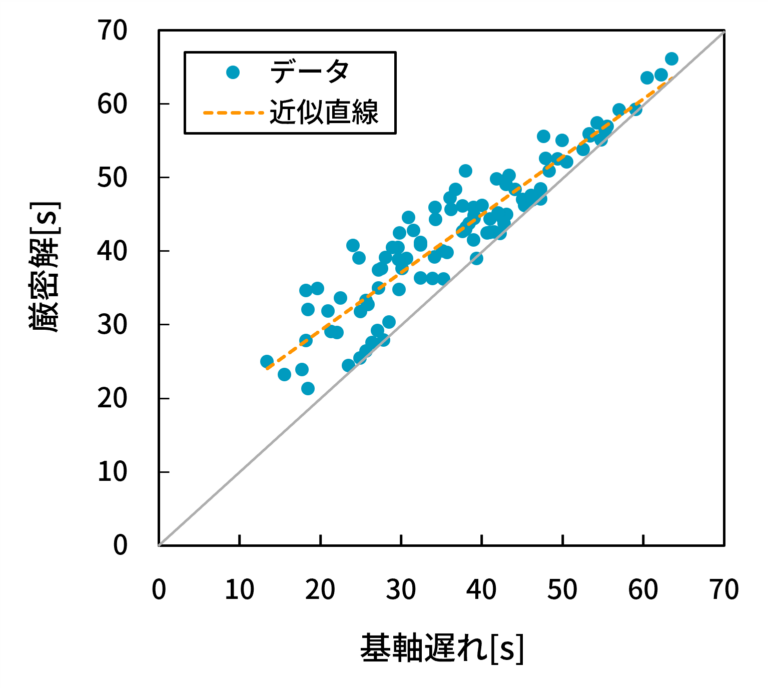
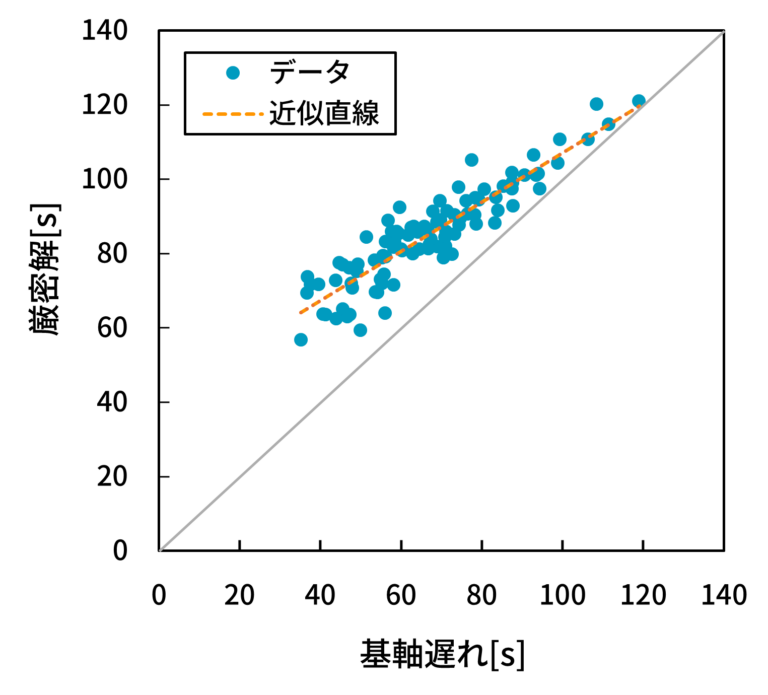
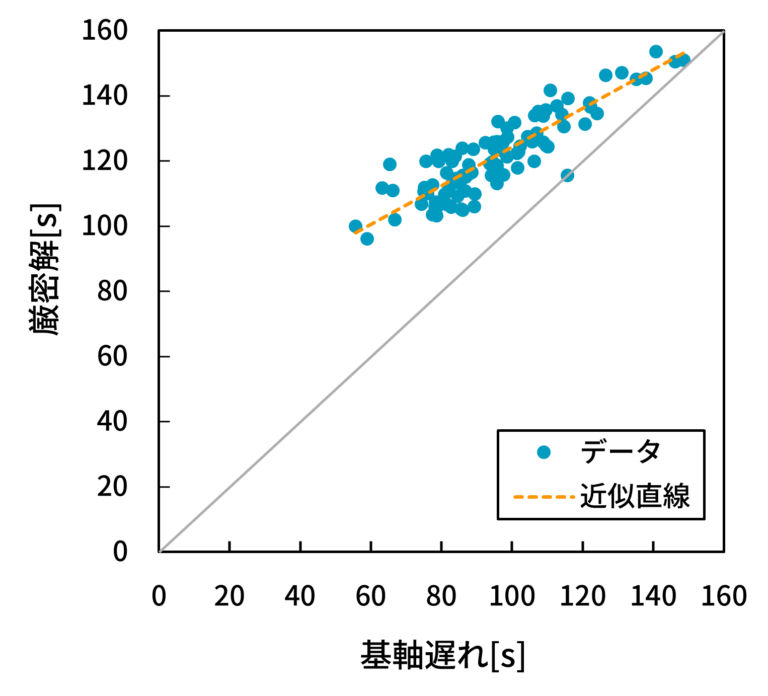
縦軸に厳密解、横軸に基軸遅れを取った散布図を図15（5交差点），図16（10交差点），図17（15交差点）に示す。グレーの45度線に近づくほど、近似誤差が小さいことを意味する。
図15, 16, 17から、基軸遅れが大きくなるほど、あるいは厳密解が大きくなるほど、近似誤差が小さくなる相関（相関係数0.9299, 0.9130, 0.8898）が存在することが分かる。

近似誤差に影響を与える路線条件の分析

ここからは、なぜ前述の関係が満たされるかを明らかにするため、近似誤差を左右する具体的な路線条件について分析する。
そこで、第2章で説明した「系統効果」と、近似誤差の関係について着目する。
- 前述したように、越は系統効果について、「高い」か「低い」かの離散的な概念として捉えていたが、本研究ではこれを連続量として扱えるようにするため、新たに「相対系統効果Δ」という指標を定義する。
- 細かい導出過程は割愛するが、この指標は(i)リンク両端の交差点の平均青時間が小さく、かつ(ii)リンク長がオフセットを適切に設定しても遅れをほとんど減らせない距離のときに、大きな値を取る指標である。
- したがって相対系統効果は、「避けられない遅れ」の絶対量であると考えられる。

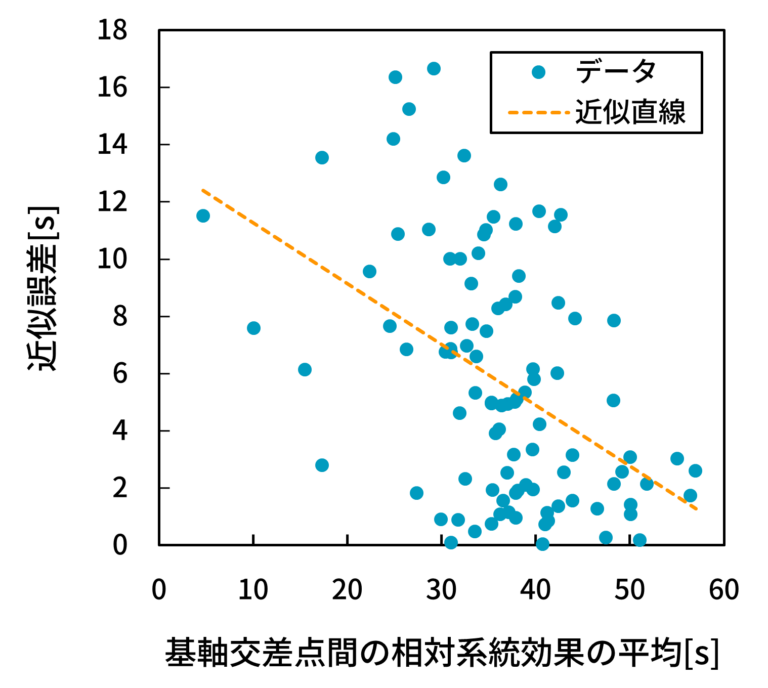
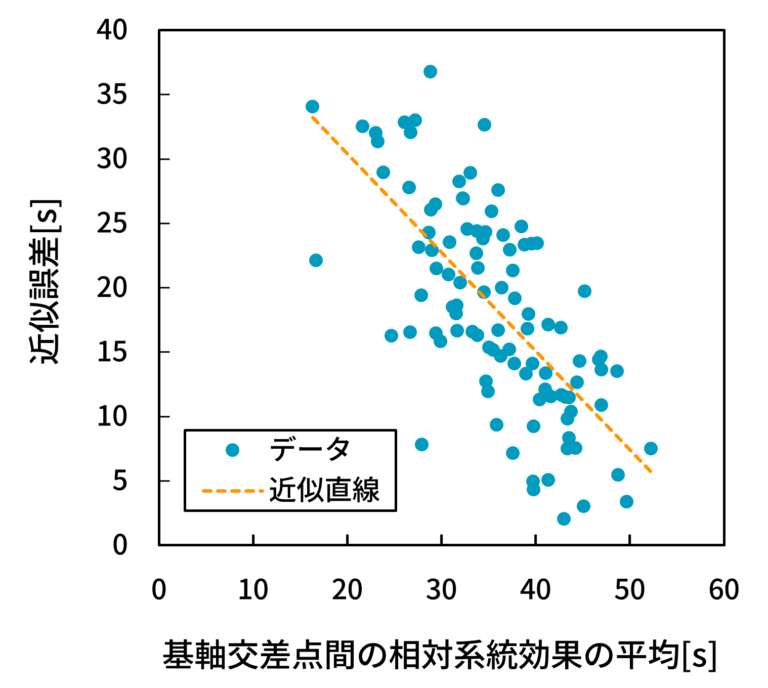
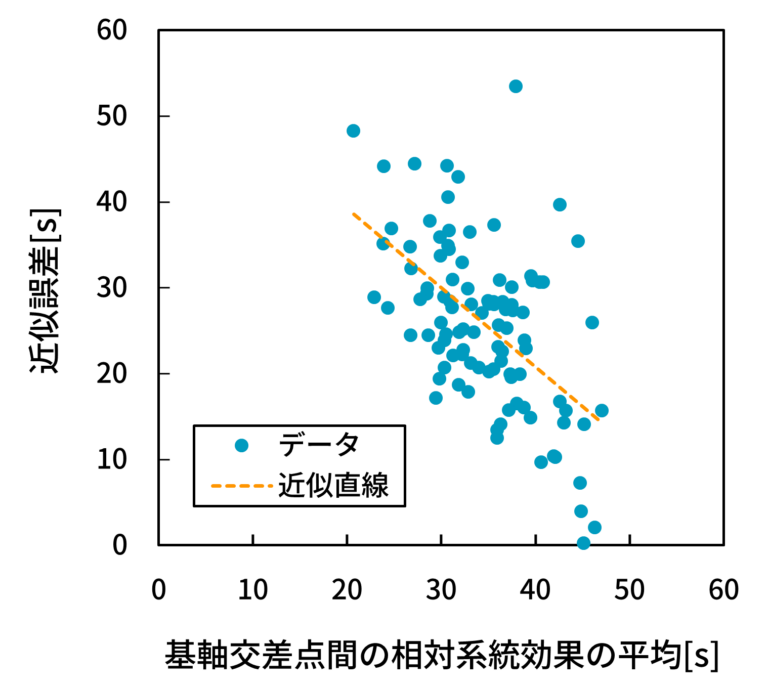
縦軸に近似誤差を、横軸に基軸交差点間の相対系統効果の平均を取った散布図を図18（5交差点），図19（10交差点），図20（15交差点）に示す。
図18, 19, 20から、近似誤差と相対系統効果の平均の間に負の相関（相関係数-0.4426, -0.6926, -0.5463）が見られることが分かる。これは、基軸交差点間の相対系統効果が平均的に大きい（i.e., オフセットを適切に設定しても遅れをほとんど減らせない）ケースでは近似誤差が小さくなり、反対に基軸交差点間の相対系統効果が平均的に小さい（i.e., オフセットを適切に設定することで遅れを十分に減らせる）ケースでは近似誤差が大きくなることを意味する。
この結果から、前者のケースでは基軸交差点にて生じる遅れのみで路線全体の最小遅れをほぼ見積もることができていること、反対に、後者のケースでは基軸交差点にて生じる遅れと最小遅れとの間に乖離があることが言える。

相対系統効果は、より簡単には青時間によって説明することができる。
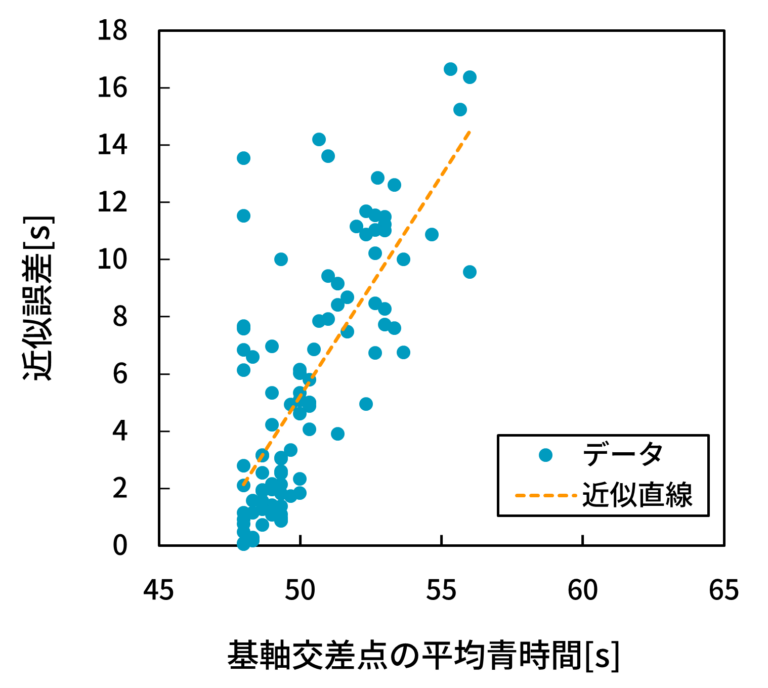
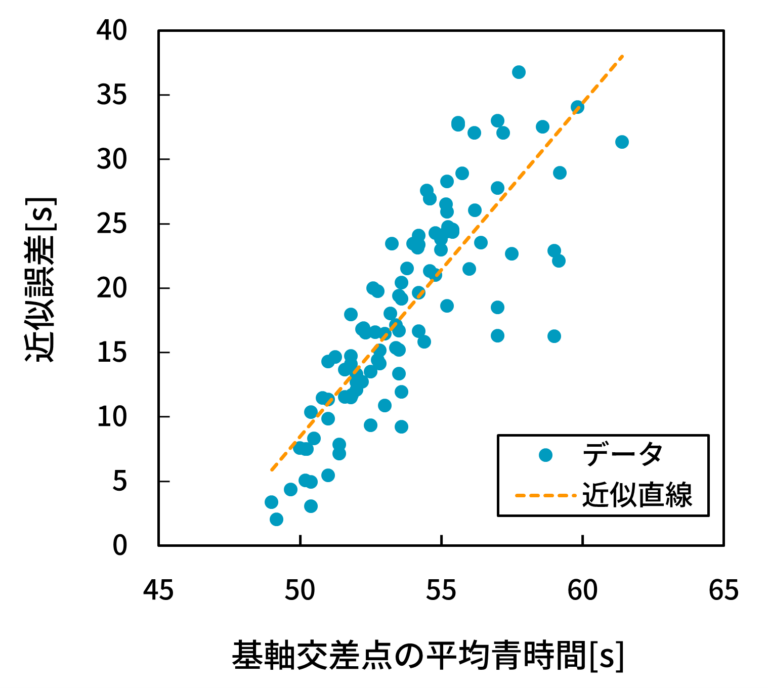
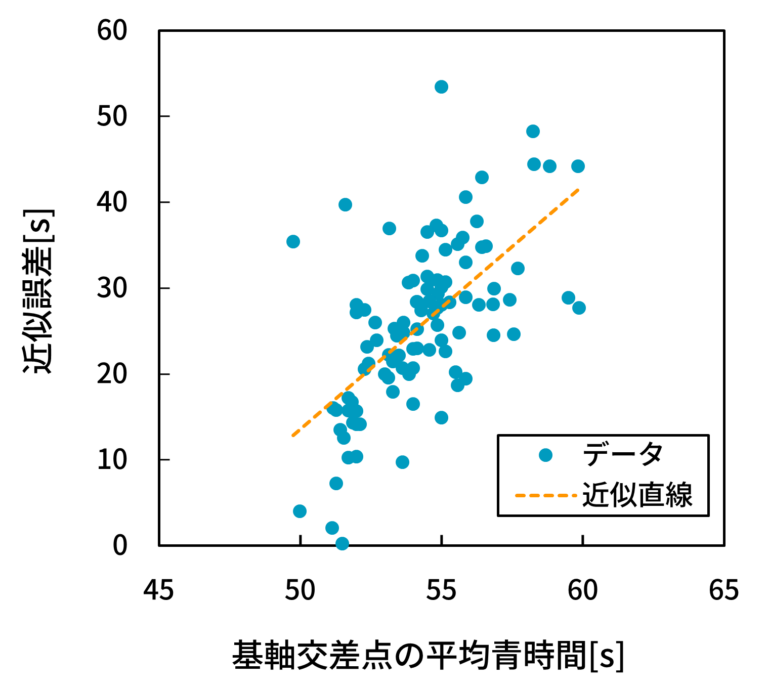
そこで、基軸交差点の平均青時間が誤差に影響を与えているかについて分析してみよう。縦軸に近似誤差を、横軸に基軸交差点の平均青時間を取った散布図を図21（5交差点），図22（10交差点），図23（15交差点）に示す。
図21, 22, 23から、基軸交差点間の平均青時間と近似誤差の間に正の相関（相関係数 0.7360, 0.8238, 0.6185）が見られることが分かる。これは、基軸交差点の平均青時間が小さいケースでは近似誤差が小さくなり、反対に平均青時間が大きいケースでは近似誤差が大きくなることを意味する。この結果から、先ほどと同様、前者のケースでは基軸交差点にて生じる遅れのみで路線全体の遅れをほぼ見積もることができていること、反対に、後者のケースでは基軸交差点にて生じる遅れと最小遅れとの間に乖離があることが言える。
第2章で説明したように、相対系統効果（より簡単には、青時間）は避けられない遅れの絶対量を説明する指標である。したがって、これを正しく推定できている路線ほど、基軸遅れの精度が高いことが明らかとなった。

まとめ

本研究では、まず榊原・大口が提唱した基軸理論の枠組みについて説明した上で、動的計画法を用いた計算の効率化手法を提案した。
次に、都市部街路を模擬した5, 10, 15交差点の計300路線を対象に、基軸理論とWada et al.に基づく厳密解法との比較分析を行い、基軸遅れの精度と、それを与える路線条件について考察した。その結果、以下のことが明らかになった。
- 最小遅れの厳密解と基軸遅れの誤差は、5交差点路線（平均路線長約600[m]）で平均6[s]程度、10交差点路線（平均路線長約1300[m]）で平均23[s]程度、15交差点路線（平均路線長約2000[m]）で平均27[s]程度であり、ほとんどの路線でサイクル長に対して40[%]程度の誤差に収まる。
- 基軸遅れが大きい路線の方が誤差が小さい（i.e., 基軸遅れの精度が高い）傾向にあり、この傾向は特に10交差点路線で顕著である。
- 基軸交差点の青時間が小さく、かつ系統効果の悪い距離関係にあるほど、誤差が小さい（i.e., 基軸遅れの精度が高い）関係にある。より簡単には、基軸交差点の青時間が小さいほど、誤差が小さい関係にある。
これらの成果から、本研究の目的である、基軸理論の有効性、現実への適用可能性が十分に示された。

参考文献

榊原肇, and 大口敬. “路線の系統制御設計妥当性評価法の一考察.” 交通工学論文集 9.3 (2023): 1-10.
越正毅. 1975. “系統交通信号におけるサイクル制御の研究.” 土木学会論文報告集 1975.241 : 125-133.
H.Sakakibara, T.Oguchi. Fundamental theory of coordination efficiency of signalized intersections on an arterial road. Transportation Research Part B(投稿中)．
Newell, Gordon F. “Theory of highway traffic signals.” ITS Reports 1989.07 (1989).
Wada, Kentaro, et al. “An optimization modeling of coordinated traffic signal control based on the variational theory and its stochastic extension.” Transportation Research Part B : Methodological 117 (2018): 907-925.

本研究を進めるにあたって、東京大学の大口敬教授、住友電工システムソリューション株式会社の榊原肇氏より路線データのサンプルをご提供いただき、また数々の貴重なコメントをいただきました。ここに記し、感謝の意を表します。

この記事は、以下の論文の一部を要約したものです。

梅村悠生. 2025. “路線分割に基づく系統制御評価とオフセット設計．” 2024年度筑波大学大学院理工情報生命学術院システム情報工学研究群社会工学学位プログラム修士論文．

編集後記

卒業論文（https://casebank.sk-tsukuba.university/case/1952）に引き続き、この度の修士論文についてもケースバンクに紹介していただけるような面白い成果を上げることができ、非常に嬉しく思います。
交通信号制御という、社会工学域としては少し特殊な研究テーマではありましたが、私なりに面白く、かつインパクトのある研究ができたと思います。
学部4年次から通算して3年間、交通システム科学研究室(Transportation System Science Lab.)の皆様に大変お世話になりました。
- 特に指導教員の和田先生には、私の未熟さゆえご迷惑をおかけすることも多々ありましたが、自分で研究に打ち込めるようになっていくにつれて、研究者としての素養が徐々に身についたのではないかと感じています。
- 後輩研究者の皆様には、まずは研究に没頭する楽しさを実感して欲しいと思います。その過程で、指導教員や研究室の仲間と「議論する楽しさ」を味わえたとき、研究者として一回り大きく成長できるのでしょうか。
3年間の研究を通して、私の人生においてかけがえのない経験をすることができました。和田先生はじめ、関係する全ての皆様に厚く御礼申し上げます。