取り組みの概要

背景と課題
- 本ケースは,高速インクジェットプリンターや、デジタル印刷機のハード及び関連機器、消耗品の開発、製造、販売を行っている理想科学工業株式会社(以下、理想科学工業)との共同プロジェクトである.
- 理想科学工業のプリンターにはエラーや故障が発生した際に事業所に通知が送られ,担当者がすぐに修理に行けるような機能が設置されている.
- エラーおよび故障が発生してから修理担当者が現場に到着するまでの間,プリンターは稼働ロス状態になってしまう.
- 事前にエラーが予測できればエラー発生前に対処を行うことで稼働ロスを削減でき,通常メンテナンス時にエラーの可能性が高い場所を点検することで,エラーの発生の防止にもつながる.
上記のような背景から,現時点でプリンターから取得できるデータを利用してエラーの予測は可能かどうかの探索を行うことが本プロジェクトの課題となる.
使用するデータ
- 今回のエラー予測にはプリンターから取得した稼働データを利用する.
- 理想科学工業のプリンターには,1枚印刷するごとに,給紙した元のトレイ,内部モータのトルク数,いくつかのポイントにおける送紙の速さとタイミング,紙に付着した堆積物の量などのデータを記録するセンサが設置されている.
- これらの稼働データから,エラー時,およびエラーの発生前特有の特徴量を検出することで,エラー発生の判別や予測ができるのではないかと考えた.
- 今回分析したデータはプリンター5台分のデータ.稼働時期は機材によって異なるが,おおよそ3か月~6か月ほどの期間の稼働データを集めたもの.
データ分析
本プロジェクトでは2つの方向からエラーの予測についての分析を実施した.
(1)エラー発生はどの程度事前に検知することが可能か
- エラーが発生する際に何らかの予兆があるとすれば,通常時と比べデータに何らかの変化があらわれるはずである.
- このデータの変化を見つけ出す手法を”変化点検知”という.
- 本プロジェクトでは機械学習を利用し,人間の目では判別しにくいデータのエラー検知を試みる.
- 機械学習には”Binary segmentation”と呼ばれる教師なし機械学習のアルゴリズムを採用した.この手法は,データの統計的性質に基づいて,変化点を検知するものである.
- 今回は提供いただいたデータから分析に使用する変数や,変化点を検知するための期間,ペナルティ値と呼ばれる機械学習モデルにおけるハイパーパラメータの設定などのさまざまな条件のもとに施行を行い,どのような条件であればエラー前に特徴的な変化点を検知できるかの探索を行った.
(2)データの特徴量からエラーの判別・予測は可能か
- 今回のデータにはエラーが発生したかどうかについても記録されているため,エラー時と通常時のそれぞれの稼働データが識別できる形で存在している.
- そのため,データの特徴量を学習させることで,エラーデータと通常データが判別できるモデルを二分決定木により作成できると考えた.
- 今回はエラー時のデータが通常時と比べ少数であったため,過学習(エラーではないデータもエラーと判断してしまう)恐れがある.そのため,複数の決定木を組み合わせる勾配ブースティングを利用した”XGBoosting”により判別モデルを作成することにした.
- 説明変数に利用する変数をさまざまな条件に基づいて組み合わせてモデルを作成し,正確性や適合率の高いモデルの探索を実施した.
成果と提案
(1)変化点の検知について
変化点を検知する上での最適な期間について
◆最も適切に変化点を検知できる期間は約1か月
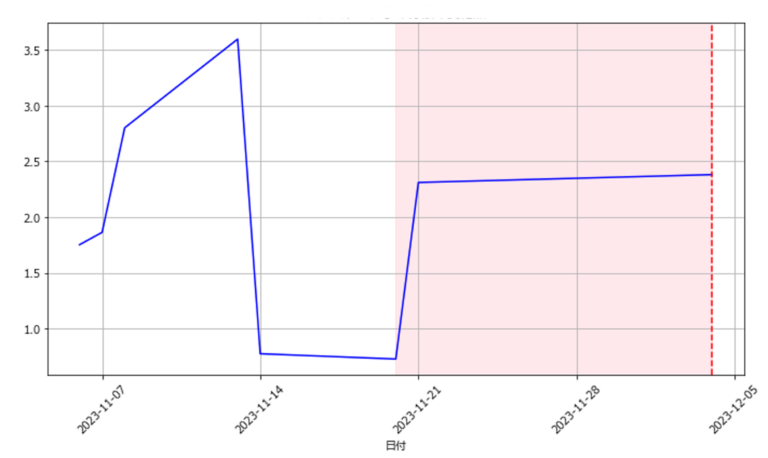
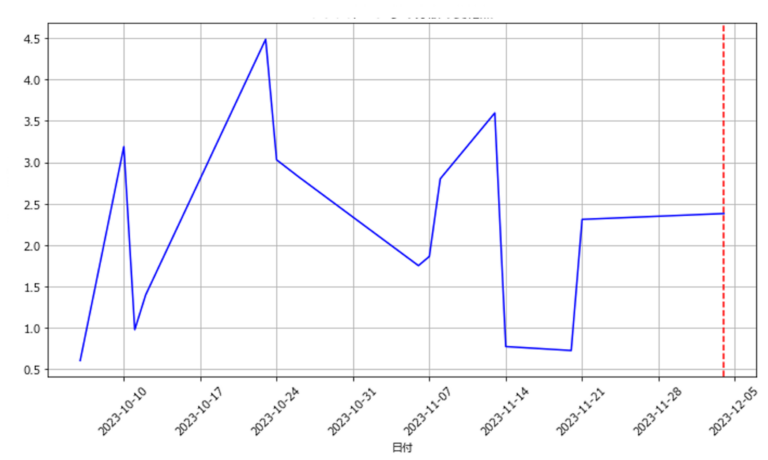
- 図2(a)(b)はエラー検知の一例である.図2(a)はあるセンサ記録した1か月分送紙速度のデータ,図2(b)はその2か月分のデータをもとに分析した結果である.それぞれ縦軸が送紙速度の分散の値,横軸が計測した日数を表す.図の背景の色が変化している点が変化点が発生した時点である.また,図中の赤い破線はエラーが発生した日にちを示している.
- 図2(a)の1か月分のデータを基にした分析では,エラーの発生した約二週間前に変化点を検知できている.
- 一方同じエラーを基準にしても,二か月分のデータを基にするとエラーを検知できない.
- 本項に示したものは一例であるが,他の変数の分散や平均値で変化点を検知した際も,1か月分のデータが最もエラー前に変化点を検知できた例が多い.
- 2か月分のデータでは,変化点が検知できなかったり,過剰に変化点を検知してしまうため適していないと考えられる.
- また,1か月より短い期間ではデータの不足により変化点が検知できない.
変化点からエラーの予測は可能か?
◆ペナルティ値の調整によってはエラー前に適切に変化点を検知できる
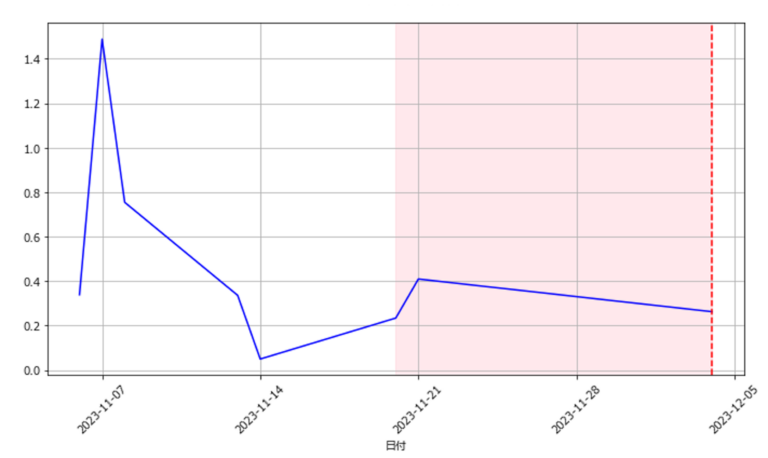
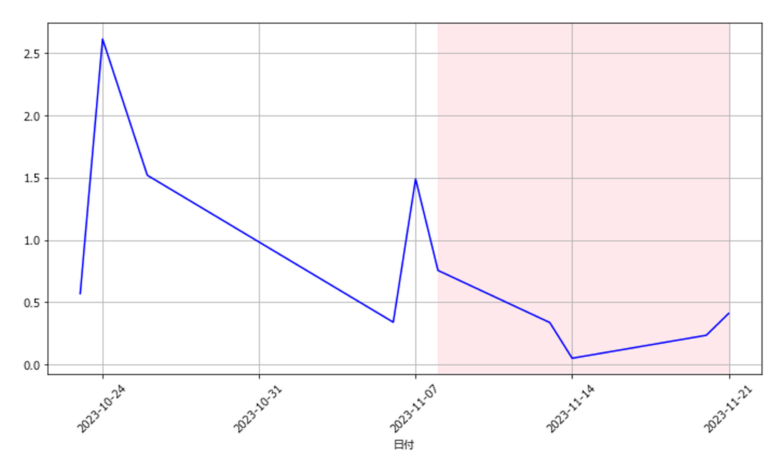
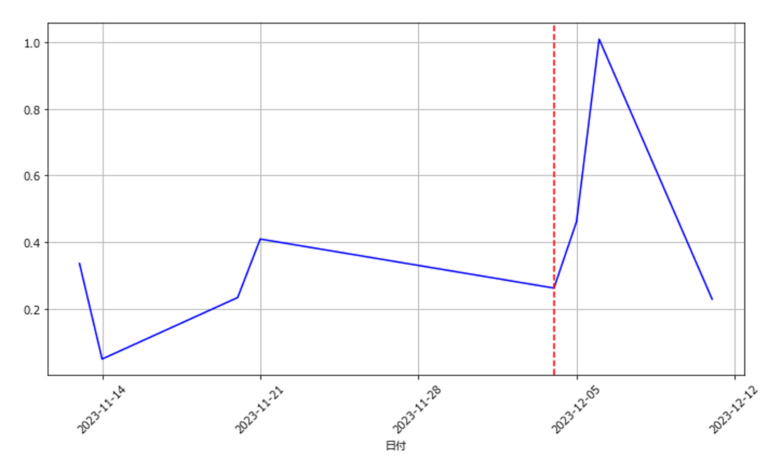
- 図3(a)(b)(c)はある機材のモータトルク数の1か月分の分散値に対してペナルティ値を8に設定した際の変化点検知の結果を示している.それぞれ縦軸がモータトルク数の分散の値,横軸が計測した日数を表す.図の背景の色が変化している点が変化点が発生した時点である.また,図中の赤い破線はエラーが発生した日にちを示している.
- 図3(a)はエラーが発生した日を基準にした変化点検知の結果である.エラー発生日のおおよそ2週間前に変化点を検知できていることが分かる.
- 図3(b)はその検知した変化点を基準にした変化点を基準にした変化点検知の結果である.こちらも変化点が始まる二週間ほど前に変化の兆候を捉えることができている.
- 一方,図3(c)のように,エラー発生後の通常運転の状態では変化点は検知できていない.これ以降の通常稼働ができている日は同様の結果が見られた.
- 以上のような結果から,今回検証した機材においては,ペナルティ値を8に設定した場合に,エラー前に変化点を検知できるといえる.
- また,他の機材では期間内に予想に適切なペナルティ値を発見することができなかった.今後学習アルゴリズムを強化し,多くのデータを学習することによって,エラー時に変化点を検知できるモデルが作成できると考えられる.
実用化に向けた提案
- 一連の分析によって,モータトルクの分散値の1か月分のデータを特定のペナルティ値で分析すると,エラーの発生前に変化点を検知できる可能性が示された.
- そのため,モータのレジスト値を常に1か月更新しながら記録するようなシステムがあれば,そのシステムで変化点を検知できた時,2週間以内にエラーが発生する可能性があるということを知ることができる.
- ただし,設定に必要なパラメータ値は機材によって異なるため,実用的な面を考えると適切なペナルティ値をフィードバックし修正するような機能も備える必要がある.
(2)エラーの判別・予測について
エラーの判別のためのアルゴリズム
- いただいた稼働データの変数を用いて,どのデータの特徴を使うことでエラーの判別ができるかどうかの分析を試みた.ところが,いただいたデータには十分な数のエラーデータが含まれておらず,クラスの不均衡問題(正常データに対してエラーデータが十分存在していないという問題)が生じていた.そのため,今回の分析では,クラスの不均衡問題をどのように解消するかが最も重要な課題となった.
- いくつかの判別アルゴリズムを試した結果,いくつかの変数によるXGBoostによる勾配ブースティングを使った判別モデルが最も精度の高い判別を可能にすることが分かった.
- なお,オーバーサンプリングとアンダーサンプリングは,ともにクラスの不均衡問題に対処するための手法である.あるクラスが他のクラスより大幅に大きいとき,少数派のサイズを拡大してバランスを取る手法がオーバーサンプリングであるのに対し,多数派のサイズを縮小してバランスを取る手法がアンダーサンプリングである.
表1 サンプリングアルゴリズムの比較
| 手法 | 初期結果 | 改善結果または特徴 |
| オーバーサンプリング(SMOTE) | エラー判別の精度: 11% リコール: 95% F1スコア: 20% | クラス1の精度: 21% F1スコア: 34% |
| アンダーサンプリング(RandomUnderSampler) | 精度: 95.56% エラー判別の精度: 21% | 大きな改善なし |
| XGBoostによる勾配ブースティング | 精度: 99.9% ROC AUC: 0.998 Gini係数: 1.0 | 高い精度と安定性を示すが過学習の可能性あり |
- ただし,XGBoostによる勾配ブースティングの手法はエラーの細かい判別ができているが,エラーの判定を行うべきでない正常なデータもエラーと判別してしまうような過学習が行われている可能性がある.
過学習を防ぐためのモデリング
- 過学習を防ぐために,いくつかモデルに組み入れる変数のパターンを変更させた3つのモデルを比較し,その精度を検証した.
- 全てのモデルに共通して投入した変数は,これまでの分析でエラー発生とある程度相関があると思われた,コピー機内の5つのセンサ(紙間,レジストセンサ,外部給紙,レジスト,透過量(給紙台))の値である.これに加え,モデル1には印刷ジョブを,モデル2には印刷枚数を,モデル3には印刷日をそれぞれ変数として加えた.
表2 各モデルの性能の比較
| モデル | 精度 | ROC AUCスコア | 特徴 |
| モデル1 (印刷ジョブを組み込み) | 98.29% | 75% | 高精度だが偽陽性が課題 |
| モデル2 (印刷枚数を組み込み) | 98.51% | 92% | クラス分離能力が改善 |
| モデル3 (印刷日を組み込み) | 97.93% | 97% | 正確なエラーの分類に 特化 |
- モデル1は精度が高いものの,正常データをエラーと検知する可能性が高く,課題のあるモデルであるといえる.
- モデル2と3は偽陽性判定の精度が改善されており,過学習を防止するモデルであるといえる.
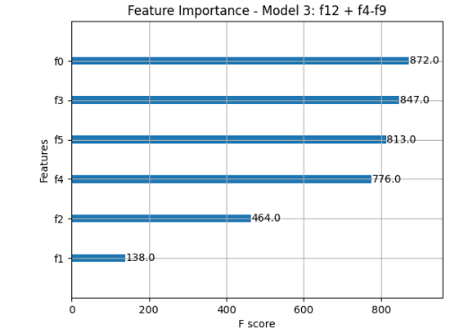
- 以下に示すグラフはモデル3におけるいくつかの変数のエラー判別に対する重要度を示したものである.これらの変数の記録を取得することで,エラー発生に対する予測が可能になることが期待できる.
凡例
F0:印刷日,F1:紙間,F2:レジストセンサ,F3:外部給紙,F4:レジスト,F5:透過量(給紙台)
- 上の図5は,上記3つのモデルのうち,最もエラーの分類に優れていたモデル3(エラー発生とある程度相関があると思われたコピー機内の5つのセンサと印刷日を変数としたモデル)における,エラー判別に対する各特徴量の重要度を示したグラフである.
- 図から,印刷日,外部給紙,透過量(給紙台),レジストの順に特徴量の重要度が高いことが読みとれる.これらのセンサの値を注視することは,実務におけるコピー機のエラー予測においても有用であると考えられる.
実用化に向けた課題
- 今回のプロジェクトでは既存のエラーを特定の変数の特徴量から判別することには成功したが,このモデルを用いて未知のデータのエラー判別までは検証できなかった.
- 今後は本モデルを基に,新たに取得したデータのエラー判別ができるようなモデルを開発していくことで,より事前の予測性の高いモデルを作成することができると考えられる.
後記
- 一連の分析を通して痛感したことは,現実のデータの扱い方の難しさについてである.多様な項目が測定されている中で,機器の使われ方を原因としてほとんど測定されていない項目や,値が計測されていてもほとんど測定値が変化していないような項目など,社会の中で実際に動いている機械ならではの,生きたデータを扱っているという実感があった.普段の研究で扱っている,シミュレーション結果や統計的な調査の結果といったデータとは異なり,データ分析しやすい形に整形するまでも労力がかかるという点は,経験が乏しかったと考えられ,何物にも代えがたい経験となった.
- 本データを提供してくださった理想科学工業様には,このような大変貴重な経験の機会を頂戴し,誠にありがとうございました.


