1．はじめに

　日本のゴミ問題で議論される内容の 1 つに、ゴミ箱が少ないということが挙げられる．これは、ゴミのポイ捨てが誘因されることが考えられる．ゴミのポイ捨ては、景観の破壊や公衆衛生の悪化を引き起こし、さらには、近年になって問題視され始めている海洋プラスチックの要因の 1 つでもある．

　特に東京などの都心部でポイ捨てされる主要なゴミは、ファストフードなどの食料包装や飲料の容器である．図 1 はそのようなポイ捨ての状況を表しており、社会問題になったタピオカの容器を中心にペットボトル、空き缶、紙コップなどが確認できる．これらのゴミは、ゴミ箱を設置し利用しやすくすることで減らすことができると考えられるため、本研究では 0-1 整数最適化問題で定式化することで最適なゴミ箱の設置台数や設置場所を求める．

2．研究の目的

　本研究ではゴミ箱の設置を数理的に最適化することで、目的を達成する上で最低限必要なゴミ箱数とその設置場所を求める．また、ゴミ箱の設置台数ごとの最適配置を比較することで、どのような場所にゴミ箱の需要が発生するかを考察する．本研究で用いるモデルは、いわゆる最大カバー問題をベースとし、ゴミの種類を新たに定義することでゴミの種類ごとのゴミ箱の配置を同時に導出している．ただし、そのまま定式化するとゴミの種類ごとに個別に解くのと同じ配置が求まるので、各設置場所に設置可能な台数の上限を定めることで「どのゴミ箱を優先するか？」といった、より現実に即したモデルを構築している．

3．モデル化とプログラムの説明

　本章では問題設定を説明し、それを基に数理モデルの解説を行う．また、実装したプログラムについても確認する．

3．1　問題設定

　本研究では、渋谷駅周辺を対象地域とする．具体的には、図 2 の黄線で囲われた部分を対象としている．ゴミの種類は、可燃ゴミ・プラスチック・空き缶の 3 種類を想定しており、それぞれ分別ができるようにゴミの種類に対応したゴミ箱を設置する．ゴミ箱の需要がある場所とゴミ箱の設置ができる場所は、実地調査と Google Map を利用して定義している．需要点の例としては、スターバックスやタピオカ専門店などのテイクアウトが利用できる店舗の周辺や、階段の下や花壇や自動販売機などのポイ捨てが発生しやすい場所、ハチ公前など人の待ち合わせがある場所などが挙げられる．また、設置候補点は、一定以上の人の往来と設置が可能な空間がある場所としている．このような問題設定で、ゴミ箱の需要をできるだけ多くカバーできるようにゴミ箱を設置していくという問題を考える．

3．2　数理モデル

　集合、定数、決定変数を以下のように定義する．

このとき、本研究では以下の最適化問題を解くことで最適なゴミ箱の配置を求めた．

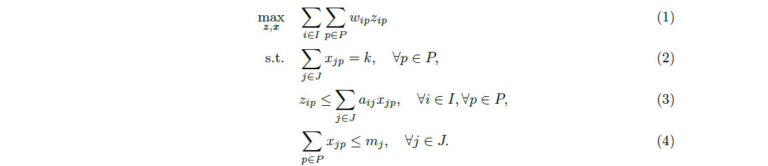
　目的関数 (1) はカバーされた需要量の最大化を意味している．制約式 (2) は各ゴミの種類に対するゴミ箱の設置台数は k 個であるという制約の下であり、k を動かしていくことによってゴミ箱が必要な場所やカバーされた需要量の推移を見ることができる．そして、制約式 (3) でカバーに関する条件を置き、制約式 (4) で各設置候補点に置けるゴミ箱の種類は m_j 以下であることを要請している．

3．3　プログラム

　最適化問題 (1)-(4) を数理最適化ソルバー FICO Xpress Optimization によって実装する． data.dat は集合 I、J、P と定数 a_ij、m_j、w_ip を格納しており、TrashBoxAllocation.mos を実行することで data.dat に応じた最適解を得ることができる．

4．データについて

　本研究で用いた集合 I、J、P と定数 a_ij、m_j、w_ip は実地調査と Google Map の情報を利用して決定した．その結果、ゴミ箱の需要点の数 |I| = 87、設置候補点の数 |J| = 93 となった．需要点 i を設置候補点 j に設置したときにカバーできるかを表す定数 a_ij は、需要点と設置候補点の距離と実地で視認できるかに基づいて決定した．また、需要点 i のゴミ p に対する需要量 w_ip は 1 から 3 の3 段階で評価した．設置候補点 j の設置可能台数も空間的な制約に基づいて決めている．

5．計算機実験の結果と考察

　本章では、実装したプログラムによって得られた結果を考察する．はじめに、各ゴミ箱の設置可能台数 k を変えて実験することで、目的関数値であるカバーされた需要量の変化を確認する．次に、ゴミ箱が設置された場所を見ることで、各ゴミ箱の需要がどのように分布しているか検討する．

5．1　設置台数の分析

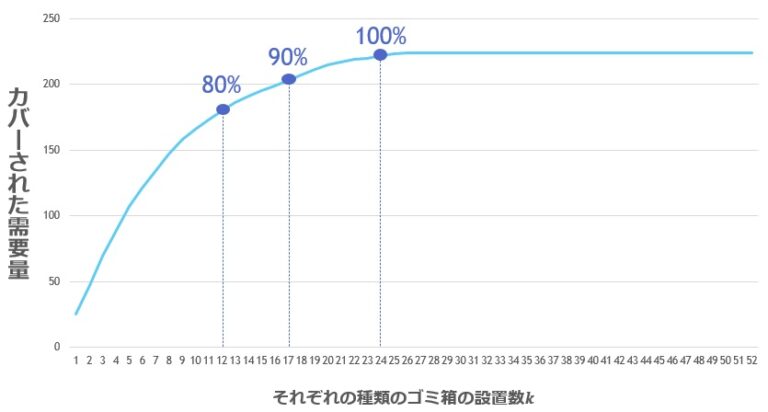
　図 3 は横軸に各ゴミ箱の設置可能台数 k を、縦軸にそのときの目的関数値であるカバーされた需要量を置いたグラフである．図中のパーセント表示は、全需要 224 のうちのカバーできた割合を表している．これより、全需要をカバーするには、多くとも 24 台ずつのゴミ箱があればよいことが分かる．さらに、80% の需要をカバーするには、100% のときのちょうど半分の 12 台ずつのゴミ箱で十分という結果となった．

5．2　設置場所の分析

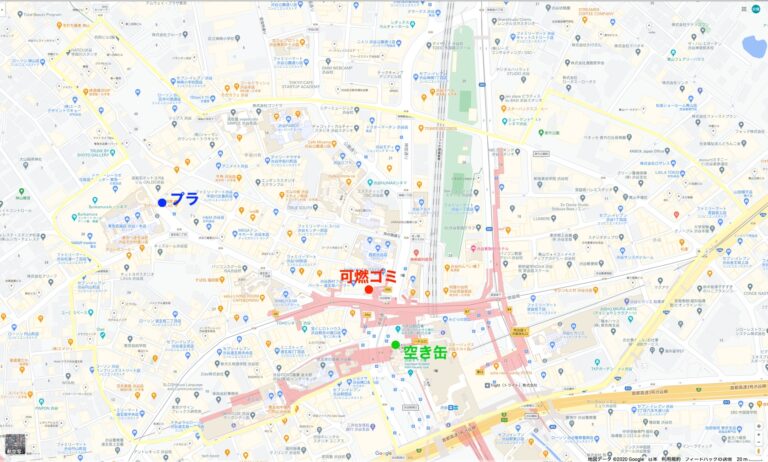
　次に、設置場所の分析を行う．図 4 は k = 1 のときに x_jp = 1 となった場所を地図上に書き込んだものである．ここから、可燃ゴミと空き缶のゴミ箱は渋谷駅近辺に設置するのが効率的であることが言える．また、プラスチック用のゴミ箱は駅から離れた場所に位置しているが、これはテイクアウトの店が集中している大通りであり、モデルが需要をうまくカバーできていることが伺える．図 5 は k = 1 のときの結果であり、渋谷駅から大通りに沿って間隔を取って並んでいることが分かる．これらの場所は図中に載せられた写真の場所と対応しており、おおよそ設置可能な場所であることが確認できる．

6．おわりに

　本研究ではポイ捨てを削減させることを目的に、最適なゴミ箱を設置を提案した．特に、最大カバー問題にゴミの種類に関する条件を加えることで異なる需要への対応を組み込んだモデルを構築し、ゴミの発生の特徴を踏まえた解釈が可能となったことである．そのため、ゴミの需要を適切に推定出来れば、その需要に応えるような配置を提案することができる．

　本研究の今後の課題として、以下の 2 つが挙げられる．1 つ目がデータが主観的に作られていることである．ある程度は指標を作ってデータを作成しているものの、「どのくらい人の往来があるか？」、「ポイ捨てが発生しやすいか？」といった定性的な評価に留まっている．そのため、需要量の推定にはアンケート調査や通行調査に基づくのが望ましい．2 つ目がゴミの回収をモデルで考慮できていないということである．本研究の結果では、大通り沿いに並んだため回収も容易であると考えられるが、運用を考慮したモデル設計に議論の余地があると考えられる．

アタッチメント