1．はじめに

　本研究は全 6 章で構成されている。第 2 章では、研究目的を説明する。第 3 章では、学校敷地内における照明設置の問題設定を紹介し、モデルを構築してモデルを実現するプログラムを説明する。第 4 章では、学校敷地内での明るくしたい場所と電気配線のある場所の位置情報や、考慮する証明の情報などのデータを説明する。第 5 章では、計算機実験の環境を紹介し、そして実験結果を分析する。第 6 章では、本研究をまとめ、そして今後の取組みについて説明する。

2．研究目的

　本研究の目的は、日立北高校の学校敷地内を最低限の照明で明るくすることである。日立北高校は、一部の敷地しか照明が設置されていないため、夜になると敷地内が全体的に暗くなるといった問題がある。中でも正門や駐車場は自転車や車などの衝突事故を発生する危険があるため、早急に解決する必要がある。また、男子テニス部のテニスコートも明かりがあまり当たっていないため、テニスコート全体を明るくするような照明が必要である。ところが、照明の設置には購入費用、工事費用、電気費用などの様々なコストが掛かるため、予算以上の照明を設置する事ができない。そのため、最低限のコストで敷地全体を明るくする照明の設置方法を考える必要がある。

3．モデル化とプログラムの説明

　本章では、学校敷地内における照明の設置問題に対し、最低限のコストで目的区域を明るくする照明設置モデルを提案し、モデルのプログラムを説明する。

3．1　問題設定

　照明が必要な区域は、学校正門辺りにある駐車場と通路、および現在照明のない男子テニスコートである。学校敷地をメッシュで表現し、さらに、学校敷地内の電気配線と障害物の位置情報を調査し、メッシュにある全ての格子に対して照明が設置できるノードの集合と照明が必要なノードの集合に分ける。三種類の照明と照明ごとの距離別照度のデータを用いている。目的区域でそれぞれの最低限の照度を確保すると同時に照明のコストを最小化する。今回高校生に調査してもらった情報には障害物の情報が入っていないが、今後障害物の情報を入れてもモデルが適用できるように、モデルでは障害物判定のパラメータを考慮している。

3．2　モデルの説明

　本節では、照明設置モデルの定式化を行う。定式化にあたり、記号の定義を以下に示す。

集合

　・I: 照明が設置できるノードの集合
　・J: 照明が必要なノードの集合
　・K: 照明の種類

定数

　・u_k: 照明 k のコスト
　・e_ij: ノード i と j 間の距離
　・b_kl: 照明 k が距離 l での照度
　・z_ij: ノード i と j 間に障害物ないならば 1，そうでないならば 0 を取るパラメータ
　・R_j: ノード j に必要な最低限の照度変数
　・v_ik ∈{0,1}: ノード i に照明 k を設置するかどうかを表す決定変数，ノード i に照明 k を設置するならば 1，そうでないならば 0 定式化

上記の定義した記号を用い、以下のようなモデルの定式化を行う。

目的関数

3．3　プログラムの説明

　本節では、前節の数理モデルを Xpress-IVE で実行するため、Mosel 言語で記述したソースコードの説明する。ソースコード 1 は全体の流れであり、declartions の中に書かれている記号は前半が最適化計算、後半が最適化の準備に用いられている。数理モデルは次の Step.1 から 4 にしたがっている。

　Step.1 　ノード集合 I,J の作成

　Step.2 　ノード間の距離 e_ij の作成

　Step.3 　ノード集合 J に必要な最低限の照度 R_j の作成

　Step.4 　最適化計算

　次にそれぞれの Step について説明を行う．

Step.1 は照明が設置できるノードの集合 I と照明が必要なノードの集合 J の大きさを数えるコードである (ソースコード 2)。Isize と Jsize はそれぞれの集合の合計数を数える変数である。Isize は照明の設置できるメッシュの左上 IMtl と右下 IMbr を用いてそれぞれの四角の面積を合計した。Jsize は照明が必要なメッシュの左上 JMtl と右下 JMbr を用いてそれぞれの四角の面積を合計した。以上により、I と J の集合を作成した。

Step.2 は照明が設置できるノードの集合 I と照明が必要なノードの集合 J の間の距離 e_ij を作るコードである (ソースコード 3)。距離 e_ij はノード i とノード j のメッシュ時の座標を用いてユークリッド距離で計算されている（ただし、ユークリッド距離は小数点以下で切り捨て）。ユークリッド距離は明かりの届く範囲を超えた場合 Lsize が渡される。Lsize は明かりが届かない場所であり、b_kl の l が Lsize であった場合、b_kl は 0 になる。Step.2 の中には障害物判定も含んでいるが、今回は障害物がなかったため、すべて1(障害物なし) で設定されている。

Step.3 は照明が必要なノード集合 J に必要な最低限の照度 R_j の作るコードである (ソースコード 5)。

R_j は Jsize の数分明かりが必要であり、それぞれの照度は RM の値以上である。

Step.4 は本数理モデルを実行するためのプログラムである (ソースコード 5)。数理モデルは前節に書かれている通りである。

4．データについて

　本章では、高校生に調査してもらった学校敷地内の情報、照明の情報、障害物の情報について述べ、それぞれの入力方法について記載する．　本章では、高校生に調査してもらった学校敷地内の情報、照明の情報、障害物の情報について述べ、それぞれの入力方法について記載する。

4．1　学校敷地内の情報

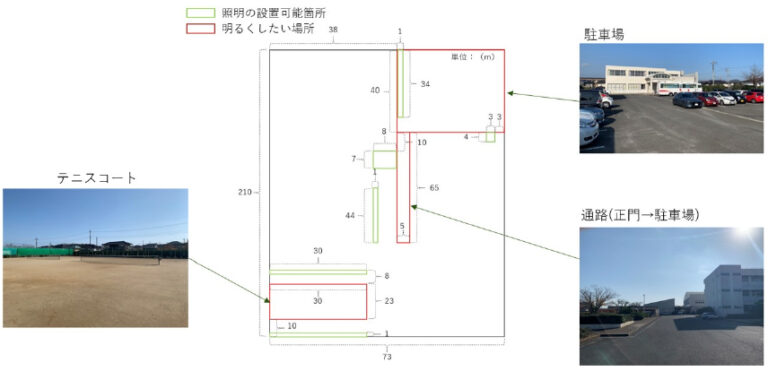
　最初に学校敷地内の情報について説明をする。学校敷地内は照明の設置できるメッシュと照明が必要な

　メッシュを調査してもらった。メッシュ 1 つのサイズは 1m × 1m である。メッシュの M = 1 が x 座標、 M = 2 が y 座標を表す。IM と JM は面積を計算する四角の数である。照明の設置できる四角の座標は左上が IMtl、右下が IMbr。照明が必要な四角の座標は左上が JMtl、右下が HMbr。敷地別の必要照度は

　RM は JM = 1(テニスコート) が 10、JM = 2(通路) が 5、JM = 3(駐車場) が 5 である。

4．2　照明の情報

　今回のモデルで考慮する照明の消費電力は表 1 に示している。表 2 と 3 に示しているのは、2 種類の照明のそれぞれの距離別照度である。今回照度は整数で表記している。また、前節の学校敷地内の情報から必要照度の最大が 10 なので、照度情報の最大も 10 に設定されている。

番号 照明の名前	消費電力 (1 時間あたり費用)
1. XY6050ZLF2 (Panasonic)	475W (12.825 円)
2. LEDG-45901N(S)-LS2 (東芝)	352W (9.504 円)

距離 (m)	照度 (lux)	距離 (m)	照度 (lux)
2	10	22	2
4	10	24	2
6	10	26	2
8	10	28	1
10	9	30	1
12	6	32	1
14	5	34	1
16	4	36	1
18	3	38	1
20	3	40	1

距離 (m)	照度 (lux)	距離 (m)	照度 (lux)
2	10	22	1
4	10	24	1
6	10	26	1
8	9	28	1
10	6	30	1
12	4	32	1
14	3	34	1
16	2	36	0
18	2	38	0
20	2	40	0

　上記の照明の情報に関するコードはソースコード 7 に示している．K は照明の番号、L は照明に明かりを届ける範囲、u は照明ごとの 1 年間の消費電力 (1 日 4 時間稼働すると仮定)、b は照明ごとの照度情報である。

4．3　障害物の情報

　モデルには障害物判定があるので、今後障害物の情報を入れることが可能である。ただし、今回は調査対象の敷地には障害物が置かれていなかったため、障害物情報は無しとする。

5．計算機実験の結果と考察

5．1　実験環境

　本章では、3 章のモデルと 4 章のデータを用いて最適化実験を行った結果を紹介する。実験環境は Intel CPU Core i5-7200U (2.5 GHz、 2 コア)、Windows 10 64bit、メモリ 16.0 GB であり、Xpress-IVE を用いて最適化を行った。

5．2　結果と考察

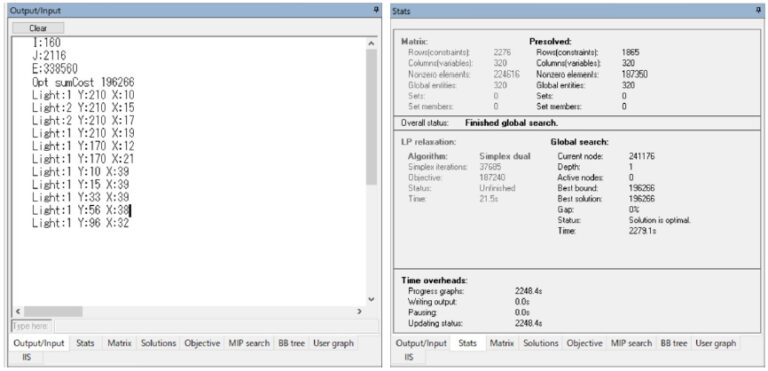
　本研究では、日立北高校の学校敷地内を最低限の照明で明るくするための最適化実験を行った。最適化実験の結果から駐車場・通路・テニスコートにおける照明の最小コストは 196266 円であった。図 2 から、照明の設置可能ノードは 160 箇所 (I = 160)、照明の必要ノードは 2116 箇所 (J = 2116)、それぞれのノードを繋ぐ距離のエッジ数 (e) は 338560 箇所であることがわかった。照明の必要ノード全体に一定以上の照度を達成するには、照明 1 を 9 箇所、照明 2 を 2 箇所設置する必要がある。図 3 の図 2 の結果をメッシュ上で表した情報から、駐車場には照明 1 を 3 箇所に設置、通路には照明 1 を 2 箇所に設置、テニスコートには照明 1 を 4 箇所、照明 2 を 2 箇所に設置するのが最適であることがわかった。

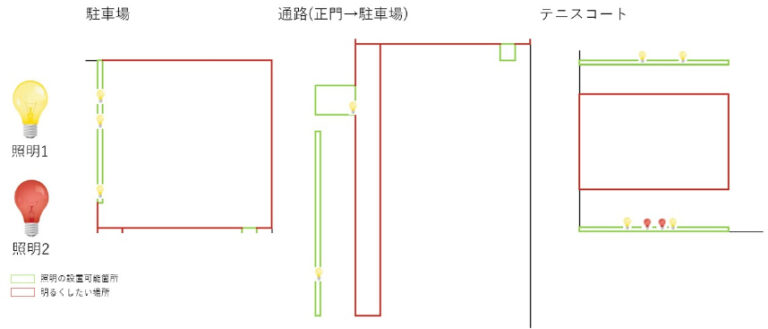
　本実験の最適化対象は、照明 1 が多く使われており、照明 2 はあまり使われていなかった。駐車場の場合、距離の都合で照明 2 で全て明るくできないといった問題があったため、照明 1 が優先されて選択されたと考えられる。通路の場合、照明 2 を 3 箇所に設置する方がコストが高く、照明 1 と 2 を 1 つずつ設置すると全体を明るくできないといった問題があったため、照明 1 は 2 箇所に設置されたと考えられる。テニスコートの場合、照明 1 だけだと明るさが足りない場所が何箇所があった。明るさの足りない場所を補うには照明 1 を 2 箇所か照明 2 を 2 箇所に設置する必要があり、コストの低い照明 2 が選択された。照明 1 と照明 2 のコストを比較すると、照明 1 を 3 箇所設置と照明 2 を 4 箇所設置はおおよそ同等の金額である。照明 2 を優先的に使用させるには、明るくしたい場所を照明 2 だけで全体が届くような問題、照明がたくさん必要な場所を問題に含むべきだったと考えられる。

6． おわりに

6．1　まとめ

　本研究では、日立北高等学校敷地内における照明の設置問題に対し、現在照明の無い学校の正門辺りにある駐車場と通路、および男子テニス部のテニスコートを明るくする照明配置案を提案するために、場所ごとの照度要求を満たし、照明費用を最小化する照明設置モデルを構築した。調査により、2 種類の照明の消費電力と距離別照度の情報、および学校敷地内で電気配線できる場所と明るくしたい場所の座標情報を獲得した。照明設置モデルをソルバー Xpress を用い、コーディングして解くことにより、最適な照明配置案を提案した。

6．2　今後の取組み

(1) 数年間の照明費用を考慮

　今回は 1 年間の照明費用で実験を行ったが、もし数年間の照明費用を考えた場合、最適化の結果がどう変化するのかを調査したい。

(2) より多くの種類の照明を考慮

現在校内では 2 種類の照明を設置すると考えたが、より効率的に校内を照らすことのできる照明を調査したい。

(3) 光害に関する制約を追加

　校内で照明を設置した場合、光害が生じる可能性がある。例えば、照明を設置する場所の近くに校舎や住宅敷地があれば、室外用の照度が高い照明はその校舎と住宅にいる人への光害源となる。モデルには、光害が生まれる可能性がある場所に対して制約を追加することによって、照明の配置案における光害の問題を有効的に解消できると考えられる。

アタッチメント