1. はじめに
現在、新型コロナウイルスが蔓延する中で、もし地震により津波が発生した場合の避難状況について、今回テーマを考えた。津波が発生し避難が必要になった場合、人々が避難所に逃げることによって、避難所内が密になってしまうおそれがある。避難所内もコロナを気にせず安全にいたいと思い、私たちは新たに避難所を追加することで密を回避しようと考えた。
2.研究の目的
避難所を追加するコストを考慮して、密の緩和に必要なだけの避難所を追加することを考えた。しかし、一部の人の避難距離だけが大きくなることは防ぎたい!故に、我々は「追加する避難所をうまく決めることで最大避難距離を最小化すること」を研究の目的とした。
3. モデル化とプログラムの説明
モデルの符号(集合・定数・変数)
● 集合
Sexisted::既存の避難所の集合
Snew::追加する避難所の候補集合
S = Sexisted ∪ Snew
V:地域集合(需要点集合)
● 定数
𝐶𝑠:避難所𝑠の本来の収容可能人数,∀𝑠 ∈ 𝑆
𝑃𝑣:地域𝑣の人数,∀𝑣 ∈ 𝑉
𝑑𝑣,𝑠:地域𝑣と避難所𝑠の距離,∀𝑣 ∈ 𝑉, 𝑠 ∈ 𝑆
𝑁:追加する避難所の上限数
𝜌:収容率
● 変数
𝐵𝑣,𝑠: 1, 𝑜𝑟 0. 地域vが避難所 sに行くかどうか,∀𝑣 ∈ 𝑉, 𝑠 ∈ 𝑆
𝑃𝐵𝑣,𝑠: 地域vが避難所s に何人行くか,∀𝑣 ∈ 𝑉, 𝑠 ∈ 𝑆
𝑦𝑠: 1, 𝑜𝑟 0. 避難所候補sを使うかどうか,∀𝑠 ∈ 𝑆𝑛𝑒𝑤
𝐷:最大避難距離
◆目的関数
Minimize 𝐷
◆制約条件

4.データについて
日立市の中でハザードマップで津波被害が想定されている地域を対象地域とし、丁町字ごとに地域を区切り、計48地域を対象としている。市が指定する避難所は86施設あり、追加する避難所の候補には避難所になっていない市内の体育館のうち,面積が分かった避難所5施設を候補とした。この5施設から必要なだけ避難所を追加する。基本的な収容人数は国の基準の3.3平方メートルあたり2人として考える。ここからできるだけ密を緩和するように、収容人数をさらに制限していく。
5.計算機実験の結果と考察
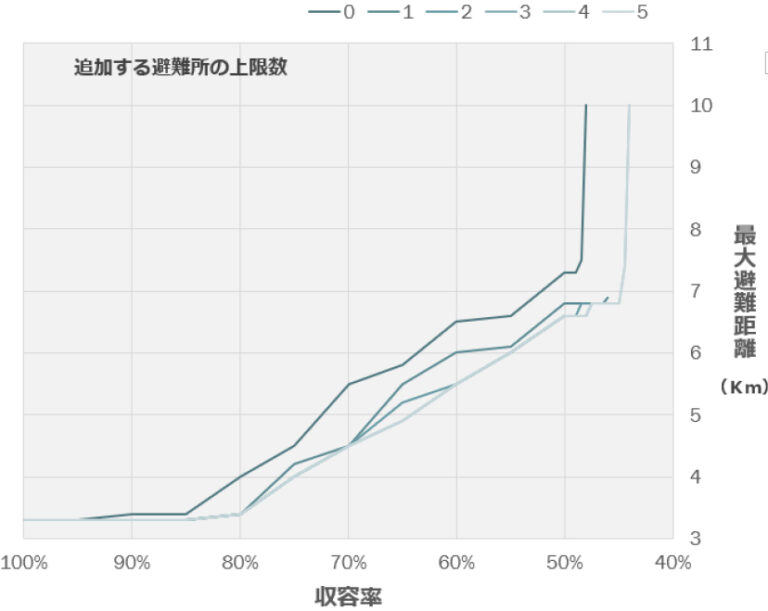
追加する避難所の上限を0~5個の範囲で収容率を40%~100%の範囲で組み合わせを色々変えて比較実験を行った。追加する避難所の上限数についてそれぞれで収容率と最大避難距離の関係をグラフにした。グラフの横軸が収容率で縦軸が避最大難距離である。
追加する避難所の上限が2以上になると収容率を変化させても最大避難距離に変化がない。収容率を85%に下回ると避難所しない場合、最大避難距離が大きくなる。つまり既存の避難所だけで一人当たり約2平方メートルはスペースが確保できる。収容率44%未満では人口の関係で実行不可能であり、今回のデータでは最大で一人当たり3.75平方メートル確保することができる。
6.おわりに
今回日立市に津波が発生した場合を想定し、避難所を追加し避難所内の収容率を下げることで密を緩和するモデルについて考えた。追加する避難所の上限数と収容率の組み合わせを変えて比較実験を行ったところ、追加する避難所の位置が近いものが多かったためか、2個以上避難所を追加しても最大避難距離がほとんど変わらない。
そのため市内様々な場所に避難所を追加する必要があることがわかった。
今後の展望として、最大避難距離をさらに短くするためにその他の体育館や避難所の新設・宿泊施設の活用を考えたい。さらに学校の教室を利用してさらなるスペースの確保をしたい。感染者が出た場合の隔離場所についても考えられる。また,他の災害の場合についても今回のモデルについて検討してみたい。
アタッチメント


