席替え革命 – 筑波大学データサイエンス・ケースバンク

１．はじめに

　学校教室における席順を最適化プログラムを用いて自動的に決定する数理モデルを提案する。教室における座席は一般的に定期的な席替えによって配置換えを行う。しかし、各座席には寒暖差があり、また黒板までの距離も異なる。したがって、席替えにおいて生徒が希望する空調状況ではない席に配置された場合、その生徒は体調を崩す可能性がある。また、視力が悪い生徒は黒板までの距離が長いと黒板を視認することが困難になる。さらに、席替えによって背の高い生徒が前方に集中すると、後方の生徒が黒板を視認することの妨げになる。

本研究では、生徒全員ができるだけ黒板が見え、希望する空調状況の席に配置することを目的とした席替えを実現するための数理モデルを提案する。提案する数理モデルを最適化プログラミングソフトウェア上で実装することにより、理想の席替えを自動的に行うことが可能になる。計算機実験では、実際にクラスの生徒の情報を収集し、理想の席順を算出することができるか最適化プログラムを試行した。

　以降本論は、研究の目的、モデル化とプログラムの説明、データについて、計算機実験の結果と考察について述べ、おわりにで全体をまとめる。

２．研究の目的

　生徒全員ができるだけ黒板が見え、希望する空調状況の席に配置することを目的とした席替えを、過去の席替えなども考慮した上で実現するための数理モデルを提案する。本モデルには以下の条件を導入する。

視力が悪く前の席を希望する場合は前の 2 行以内に配置
できるだけ希望する空調状況の座席に配置
前の席の生徒が自身より 5cm 以上高くならない
前後左右の座席に異性しかいない状況を避ける
過去に近くの席 (前後左右) に座った人と再び近くにならないまた本モデルが想定する教室の設定は以下の通りである．
クラスの生徒数は 42 人
座席の配置は 7 行 6 列
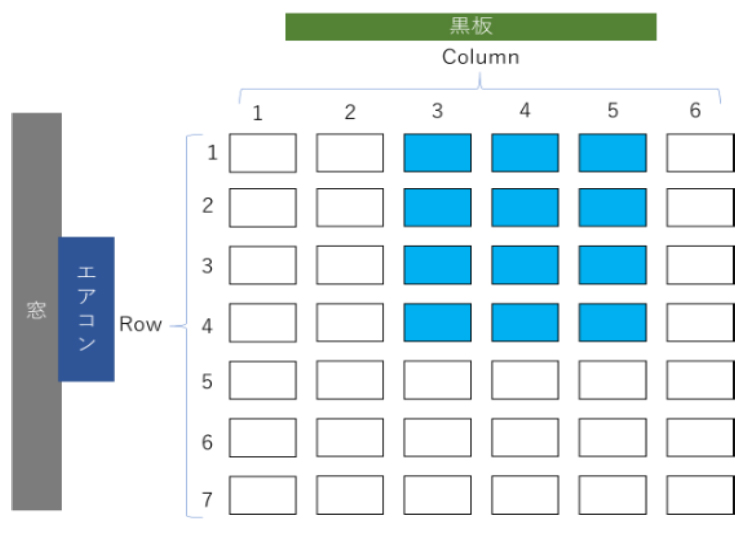
冷房器具の風が届く席は事前に調査済み (図 1)

3．モデル化とプログラムの説明

　本節ではモデル化した際の集合および定数と決定変数、目的関数、制約条件、またプログラムの説明について示す。

3．1　集合・定数

　教室の座席の行をRow、座席の列をColumn、生徒の番号をN、女子生徒の番号をF として持つ集合を定義する。また各定数len_n、es_n、nac_n、fac_n、C_n、M を定義する。以降、冷房のあたる席を涼しい席、あたらない席を寒くない席と呼ぶこととする。

3．2　決定変数

各決定変数x_i,j,n、y_i,j 、v_n、w_n、z_n を定義する。

3．3　目的関数・制約条件

式 1 から式 26 に目的関数と制約条件、またそれらの説明について示す。

3．4　プログラムの説明

　本研究では、最適化ソフトウェアとして FICO Xpress Optimization [1] を用いた。したがって、プログラミング言語は Xpress Mosel [2] で記述した。前述の数理モデルを実装したプログラムをソースコード 1 に示す。数理モデルの各式との対応付けは、ソースコード内のコメントアウト上に記述する。

ソースコード 1 提案する数理モデルを実装したプログラム。コメントシンタックスは (! コメント !)。

４．データについて

　提案したモデルを実行するためには、クラスの生徒の空調状況の希望や身長などの情報が必要である。各情報については紙面によるアンケートを用いて収集した。収集に用いたアンケートを図 2 に、収集したデータを表 1 に示す。

出席番号	性別	身長	前の席を希望するか否か	冷房が当たる席を希望するか否か
1	女	162.5	×	どちらでもよい
2	男	173.6	×	どちらでもよい
3	女	156.3	×	どちらでもよい
4	男	181.3	×	希望する
5	女	154.8	×	希望しない
6	女	152.8	×	希望する
7	男	169.4	〇	どちらでもよい
8	男	175.5	×	希望しない
9	男	178	×	どちらでもよい
10	男	170.4	×	希望しない
11	女	149.8	×	希望しない
12	男	173.4	×	希望する
13	男	162.5	×	希望しない
14	男	161	×	どちらでもよい
15	男	176.5	×	どちらでもよい
16	男	181	×	希望しない
17	女	159	×	どちらでもよい
18	女	157.6	×	どちらでもよい
19	女	75.2	×	希望しない
20	女	166.8	×	希望しない
21	女	153.2	×	どちらでもよい
22	男	169.2	×	どちらでもよい
23	男	182	×	希望する
24	女	160.5	×	どちらでもよい
25	女	160.5	×	希望しない
26	女	159.8	×	希望しない
27	女	157	×	どちらでもよい
28	男	160.5	×	どちらでもよい
29	女	156.6	×	どちらでもよい
30	男	171	×	どちらでもよい
31	女	154.5	×	どちらでもよい
32	男	164.1	×	どちらでもよい
33	男	168.5	×	どちらでもよい
34	男	156.8	〇	希望しない
35	女	156	×	希望しない
36	男	182.9	×	希望しない
37	男	172.3	×	どちらでもよい
38	女	154.1	×	どちらでもよい
39	男	168.8	×	希望しない
40	男	172.9	×	希望しない
41	女	150.3	×	希望しない
42	男	162	×	希望しない

表 1 アンケートを用いて収集したデータ

5．計算機実験の結果と考察

計算機実験の結果として、席替え 3 回分の結果をそれぞれ、初回を図 3、2 回目を図 4、3 回目を図 5 に示す。

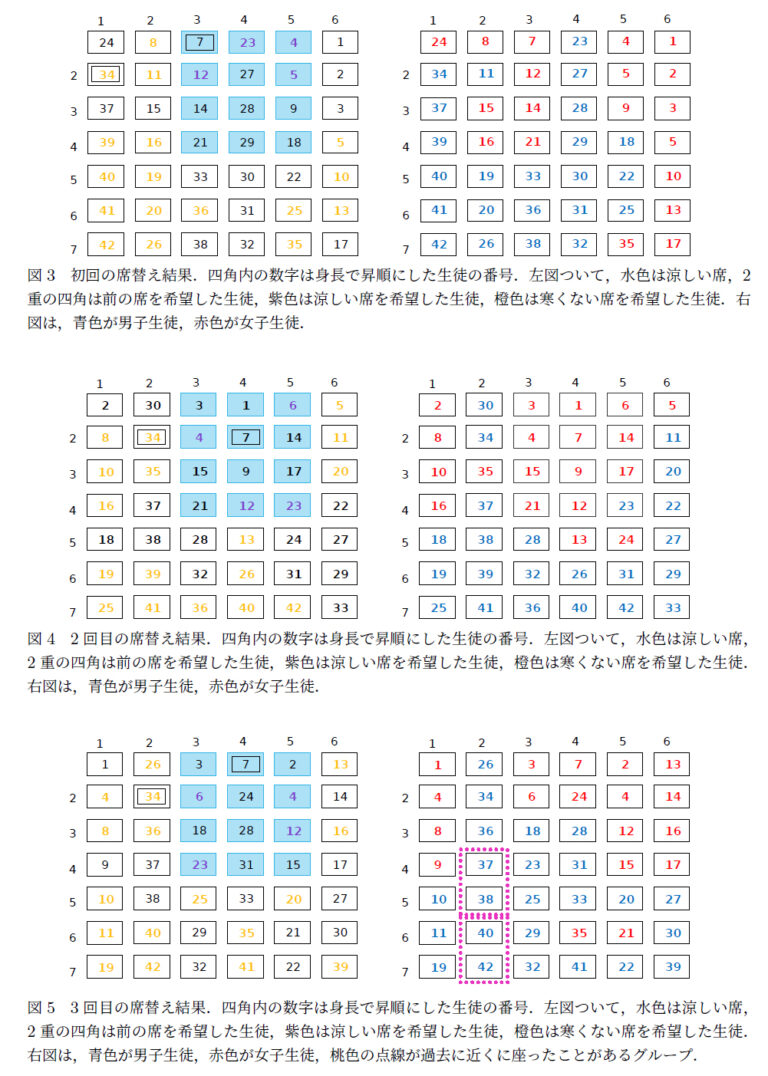
　目的関数値はそれぞれ、初回は 0.0、2 回目は 0.0、3 回目は 0.4 であった。

　今回行った 3 回の実験において、視力と空調状況の希望は全て反映した席配置で導出できた。これは対象としたクラスに視力の悪い生徒と、涼しい席を希望する生徒が少なかったことが原因だと考えられる。しかし、視力については矯正することで解決する場合が多いため、一定以上になることはないと考えられるが、空調状況の希望は場合によって異なる可能性が大きい。したがって、涼しい席を希望する生徒が多くなった場合についても対応できるようモデルを改良する余地はある。

　また、全体的に女子生徒が前の方に配置される傾向があった。これは女性の平均身長は男性の平均身長より低いという前提条件がある上で、身長を制約条件に含めた結果である。

6．おわりに

　本研究では、生徒全員の様々な希望や制約に応えた席配置をすることを目的とした席替えを実現するための数理モデルの提案を行った。提案モデルを用いた席替えのシミュレーションでは、空調の希望、視力、身長、性別、これまでの席配置といったデータを実在するクラスを対象にアンケート調査で収集し、計算機実験を行った。計算機実験では、以下のような結果が得られた。

前の座席を希望する生徒と涼しい席を希望する生徒の人数が少なかったため、視力と空調状況の希望を完全に考慮する座席配置を 3 回作ることができた。

基本的に身長が低い生徒から前の座席に配置されているため、女子生徒が前方の座席に固まることが多い。

　今後は 42 人以外の生徒数のクラスへの対応や、空き席に対する光の影響や、前後左右だけではなく斜めの座席も考慮した席替えを行えるようにすることで、より多くの人のニーズに応えられるモデルを提案したい。

参考文献

[1] FICO. (2021). “FICO Xpress Optimization.” Retrieved from https://www.fico.com/en/products/fico-xpress-optimization
[2] Neill Crossley. (2018).“FICO Xpress Mosel Introductory Tutorial.” Retrieved from https://community.fico.com/docs/DOC-3787

アタッチメント

データセット

分析用コード